【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).

(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
参考答案:
【答案】(1)见解析;
(2)①8;②t=![]() 或y=
或y=![]() .
.
【解析】
(1)判断出△ADE≌△CDF得出AE=CF,即可得出结论;
(2)①先求出AC=BC=8,进而判断出AE=CF=AC=8,即可得出结论;
②先判断出△ACE和△ACF的边AE和CF上的高相等,进而判断出AE=2CF,再分两种情况,建立方程求解即可得出结论.
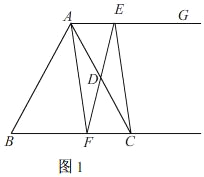
解:(1)如图1.
∵AG∥BC,
∴∠EAC=∠FCA,∠AED=∠CFD.
∵EF经过AC边的中点D,
∴AD=CD,
∴△ADE≌△CDF(AAS),
∴AE=CF.
∵AE∥FC,
∴四边形AFCE是平行四边形;
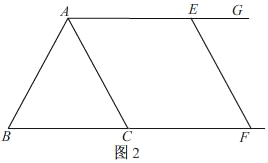
(2)①如图2.
∵△ABC是等边三角形,
∴AC=BC=8.
∵四边形ACFE是菱形,
∴AE=CF=AC=BC=8,且点F在BC延长线上,由运动知,AE=t,BF=2t,
∴CF=2t﹣8,t=8,将t=8代入CF=2t﹣8中,
得CF=8=AC=AE,符合题意,即:t=8秒时,四边形ACFE是菱形.
故答案为:8;
②设平行线AG与BC的距离为h,
∴△ACE边AE上的高为h,△ACF的边CF上的高为h.
∵△ACE的面积是△ACF的面积的2倍,
∴AE=2CF,当点F在线段BC上时(0<t<4),CF=8﹣2t,AE=t,
∴t=2(8﹣2t),
∴![]()
当点F在BC的延长线上时(t>4),CF=2t﹣8,AE=t,
∴t=2(2t﹣8),
∴![]()
即:t=![]() 秒或
秒或![]() 秒时,△ACE的面积是△ACF的面积的2倍.
秒时,△ACE的面积是△ACF的面积的2倍.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把对角线相等的四边形叫做和美四边形.
 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子. 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形; 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O, ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
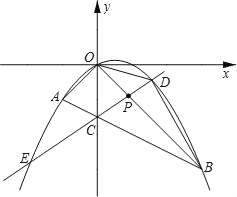
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)解方程组:
①

②

(2)计算
①(π-2013)0-(
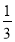 )-2+|-4|;
)-2+|-4|;②4(a+2)(a+1)-7(a+3)(a-3)
(3)因式分解
①a4-16
②

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.

试说明:AC∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, ,中位线
,中位线 与对角线
与对角线 交于
交于 两点,若
两点,若 cm,
cm,  cm,则
cm,则 的长等于( )
的长等于( )
A. 10 cm B. 13 cm C. 20 cm D. 26 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.

利用数形结合思想回答下列问题:
①数轴上表示1和3两点之间的距离是
②数轴上表示x和-1的两点之间的距离表示为
③若x表示一个有理数,且-4<x<2,则|x-2|+|x+4|=
④若x表示一个有理数,且|x-2|+|x+4|=8,则有理数x的值是
相关试题

