【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少?
参考答案:
【答案】
(1)解:如图,以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
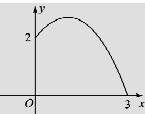
由题意可设抛物线的函数解析式为y=a(x-1)2+h(0≤x≤3)
抛物线过点(0,2)和(3,0),代入抛物线解析式得:
![]()
解得: 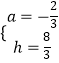
所以,抛物线的解析式为:y=- ![]() (x-1)2+
(x-1)2+ ![]() (0≤x≤3),
(0≤x≤3),
化为一般形式为:y=- ![]() (0≤x≤3)
(0≤x≤3)
(2)解:由(1)知抛物线的解析式为y=- ![]() (x-1)2+
(x-1)2+ ![]() (0≤x≤3),
(0≤x≤3),
当x=1时,y= ![]() ,
,
所以,抛物线水柱的最大高度为 ![]() m.
m.
【解析】(1)坐标原点可设在特殊位置,以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系,设抛物线的解析式可设成顶点式,,代入(0,2)和(3,0)得出方程组,解方程组即可;(2)最值问题,可运用配方法,在自变量的取值范围内,顶点的纵坐标就是最大值,求出当x=1时,y=![]() .
.
【考点精析】根据题目的已知条件,利用二次函数的最值的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置……以此类推,这样连续旋转2018次后,顶点A在整个旋转过程中所经过的路线之和是

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:给定两个不等式组
 和
和 ,若不等式组
,若不等式组 的任意一个解,都是不等式组
的任意一个解,都是不等式组 的一个解,则称不等式组
的一个解,则称不等式组 为不等式组
为不等式组 的“子集”例如:不等式组:
的“子集”例如:不等式组: 是:
是: 的“子集”.
的“子集”.(1)若不等式组:
 ,
, ,其中不等式组_________是不等式组
,其中不等式组_________是不等式组 的“子集”(填
的“子集”(填 或
或 );
);(2)若关于
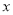 的不等式组
的不等式组 是不等式组
是不等式组 的“子集”,则
的“子集”,则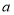 的取值范围是________;
的取值范围是________;(3)已知
 为互不相等的整数,其中
为互不相等的整数,其中 ,
, ,下列三个不等式组:
,下列三个不等式组: ,
, ,
, 满足:
满足: 是
是 的“子集”且
的“子集”且 是
是 的“子集”,则
的“子集”,则 的值为__________;
的值为__________;(4)已知不等式组
 有解,且
有解,且 是不等式组
是不等式组 的“子集”,请写出
的“子集”,请写出 ,
, 满足的条件:________________.
满足的条件:________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC
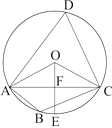
(1)求∠OCA的度数
(2)如果OE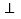 AC于F,且OC=
AC于F,且OC= 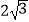 , 求AC的长
, 求AC的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按 元销售时,每天可销售
元销售时,每天可销售  个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出  个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为  元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润  元?
元? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式:2x﹣5<4(x+1)﹣3;
(2)解关于x的不等式:x﹣5>a(x+4)(a≠1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于结论:当a+b=0时,a3+b3=0也成立.若将a看成a3的立方根,b看成b3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两个数也互为相反数”
(1)举一个具体的例子来判断上述结论是否成立;
(2)若
 和
和 互为相反数,且x+5的平方根是它本身,求x+y的立方根.
互为相反数,且x+5的平方根是它本身,求x+y的立方根.
相关试题

