【题目】(1)解不等式:2x﹣5<4(x+1)﹣3;
(2)解关于x的不等式:x﹣5>a(x+4)(a≠1).
参考答案:
【答案】(1)x>﹣3;(2)当a>1时,不等式的解集为x<![]() ;当a<1时,不等式的解集为x>
;当a<1时,不等式的解集为x>![]()
【解析】
(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得.
(2)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得,其中系数化为1时需要对x的次数进行分类讨论.
解:(1)2x﹣5<4x+4﹣3,
2x﹣4x<4﹣3+5,
﹣2x<6,
x>﹣3;
(2)x﹣5>ax+4a,
x﹣ax>4a+5,
(1﹣a)x>4a+5,
①当a>1时,1﹣a<0,则不等式的解集为x<![]() ;
;
②当a<1时,1﹣a>0,则不等式的解集为x>![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD 是⊙O的内接四边形,∠ABC=2∠D,连接OA,OC,AC
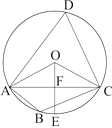
(1)求∠OCA的度数
(2)如果OE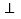 AC于F,且OC=
AC于F,且OC= 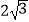 , 求AC的长
, 求AC的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.

(1)请你建立适当的平面直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度的多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按 元销售时,每天可销售
元销售时,每天可销售  个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出  个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为  元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润  元?
元? -
科目: 来源: 题型:
查看答案和解析>>【题目】对于结论:当a+b=0时,a3+b3=0也成立.若将a看成a3的立方根,b看成b3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两个数也互为相反数”
(1)举一个具体的例子来判断上述结论是否成立;
(2)若
 和
和 互为相反数,且x+5的平方根是它本身,求x+y的立方根.
互为相反数,且x+5的平方根是它本身,求x+y的立方根. -
科目: 来源: 题型:
查看答案和解析>>【题目】某年级共有300名学生,为了解该年级学生在
 ,
, 两个体育项目上的达标情况,进行了抽样调査.过程如下,请补充完整.
两个体育项目上的达标情况,进行了抽样调査.过程如下,请补充完整.收集数据从该年级随机抽取30名学生进行测试,测试成绩(百分制)如下:
 项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74
项目 78 86 74 81 75 76 87 49 74 91 75 79 81 71 74 81 86 69 83 77 82 85 92 95 58 54 63 67 82 74 项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75
项目 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 100 70 40 84 86 92 96 53 57 63 68 81 75整理、描述数据
 项目的频数分布表
项目的频数分布表分组
划记
频数

—
1


2


2



8



5
(说明:成绩80分及以上为优秀,60~79分为基本达标,59分以下为不合格)
根据以上信息,回答下列问题:
(1)补全统计图、统计表;
(2)在此次测试中,成绩更好的项目是__________,理由是__________;
(3)假设该年级学生都参加此次测试,估计
 项目和
项目和 项目成绩都是优秀的人数最多为________人.
项目成绩都是优秀的人数最多为________人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型
B型
价格(万元/台)
x
y
年载客量/万人次
60
100
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?
相关试题

