【题目】如图,已知AD为等腰三角形ABC的底角的平分线,∠C=90°,求证:AB=AC+CD. 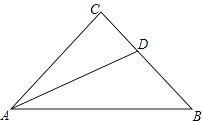
参考答案:
【答案】证明:作DE⊥AB于E,
∵△ABC是等腰直角三角形,
∴∠B=45°,又DE⊥AB,
∴DE=BE,
∵AD为△ABC的底角的平分线,∠C=90°,DE⊥AB,
∴DE=DC,
则CD=BE,
在△CAD和△EAD中,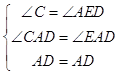 ,
,
∴△CAD≌△EAD,
∴AC=AE,
AB=AE+EB=AC+CD.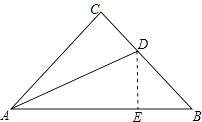
【解析】作DE⊥AB于E,根据等腰三角形的性质证明DE=BE,根据角平分线的性质得到CD=DE,证明△CAD≌△EAD,得到AC=AE,得到答案.
【考点精析】关于本题考查的等腰直角三角形和角平分线的性质定理,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要了解一个城市的气温变化情况,下列观测方法最可靠的一种方法是( )
A. 一年中随机选中20天进行观测
B. 一年中随机选中一个月进行连续观测
C. 一年四季各随机选中一个月进行连续观测
D. 一年四季各随机选中一个星期进行连续观测
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校学生会组织学生到距学校6千米的敬老院打扫卫生,如图所示,11、12分别表示步行和骑车同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,求在距学校多远处骑车的同学追上步行的同学,此时步行的同学走了多少分钟?
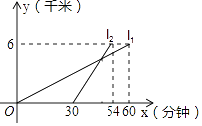
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,0)、B(b,0),且
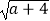 +|b﹣2|=0.
+|b﹣2|=0. 
(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的 ?若存在,求出点D的坐标;若不存在,请说明理由.
?若存在,求出点D的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是( )
A. 打开电视机正在播放广告B. 投掷一枚质地均匀的硬币100次,正面向上的次数为50次
C. 任意画一个三角形,其内角和为180°D. 任意一个二次函数图象与x轴有交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC,D为垂足,DE∥AB,∠1=∠2,图中EF与BC垂直吗?为什么?
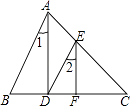
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.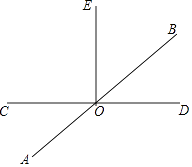
相关试题

