【题目】如图1,抛物线![]() ,其中
,其中![]() ,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
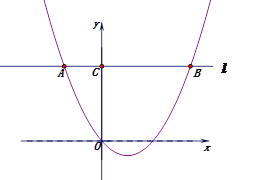
(1)求m的值.
(2)当a=2时,求点B的坐标.
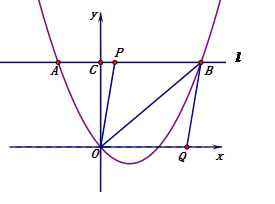
(3)如图2,以OB为对角线作菱形OPBQ,顶点P在直线l上,顶点Q在x轴上.
①若PB=2AP,求a的值.
②菱形OPBQ的面积的最小值是 .
参考答案:
【答案】(1)当x=-2时,y=4a-4(a-1)=4(2)点B的坐标为(1,4)(3)①![]() ②菱形的最小面积=16
②菱形的最小面积=16
【解析】(1)把x=-2代入抛物线![]() 即可得到y的值;(2)先求出抛物线表达式,然后求出x的解;(3)利用抛物线的对称轴即可求出点B的坐标和a的值以及菱形OPBQ的面积的最小值.
即可得到y的值;(2)先求出抛物线表达式,然后求出x的解;(3)利用抛物线的对称轴即可求出点B的坐标和a的值以及菱形OPBQ的面积的最小值.
解:(1)当x=-2时,![]()
(2)当a=2时,抛物线表达式为![]()
当y=4时,![]() ,
,
解得![]()
把-2舍去,点B的坐标为(1,4)
(3)①当点P在线段AB上时,设CP=x,则AP=2+x,BP=OP=4+2x
在Rt△OCP中,![]() ,
,
解得![]()
∴CP=0,CB=PB=4,点B的坐标是(4,4)
由题可知抛物线的对称轴:直线![]()
又由点A与点B关于对称轴对称,则![]() ,解得
,解得![]()
当点P在射线BA上时,设CP=x,则AP=x-2,BP=OP=2x-4
在Rt△OCP中, ![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
∴CP=![]() ,PB=
,PB=![]() ,CB=
,CB=![]() 点B的坐标是(
点B的坐标是(![]() ,4)
,4)
由点A与点B关于对称轴对称,则 ,解得
,解得![]()
②菱形的最小面积=16
“点睛”本题考查待定系数法确定二次函数解析式、二次函数性质等知识,解题的关键是由点A与点B关于对称轴对称求出a的值,会运用方程的思想解决问题,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,以AB为直径作⊙O分别交AC,BC于点D,E,且
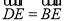

(1)求证:AB=AC.
(2)若∠C=70°,求
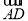 的度数.
的度数.(3)如图2,点F在⊙O上,
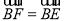 ,连结DF,DE.求证:∠ADF=∠CDE.
,连结DF,DE.求证:∠ADF=∠CDE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式成立的是( )
A.a﹣(b+c)=a﹣b+c
B.a+b﹣c=a+(b﹣c)
C.a+(b+c)=a﹣b+c
D.a+b﹣c=a﹣(b+c) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )

A.2
B.2
C.4
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在⊙O上.(不限画图工具,要保留作图痕迹)

(1)作⊙O的内接正三角形ABC.
若⊙O的半径为6,则S扇形OAB=____ ____ .
-
科目: 来源: 题型:
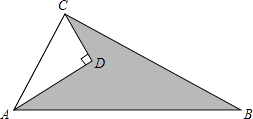
查看答案和解析>>【题目】已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各数:1,2,5,14 …,按你发现的规律计算这列数的第5个数为_______________
相关试题

