【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( ) 
A.2 ![]()
B.2
C.4 ![]()
D.4
参考答案:
【答案】A
【解析】解:∵在Rt△ABC中,∠B=90°,∠A=30°, ∴∠ACB=60°,
∵DE垂直平分斜边AC,
∴AD=CD,
∴∠ACD=∠A=30°,
∴∠DCB=60°﹣30°=30°,
在Rt△DBC中,∠B=90°,∠DCB=30°,BD=1,
∴CD=2BD=2,
由勾股定理得:BC= ![]() =
= ![]() ,
,
在Rt△ABC中,∠B=90°,∠A=30°,BC= ![]() ,
,
∴AC=2BC=2 ![]() ,
,
故选A.
求出∠ACB,根据线段垂直平分线的性质求出AD=CD,推出∠ACD=∠A=30°,求出∠DCB,即可求出BD、BC,根据含30°角的直角三角形性质求出AC即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级“诗歌大会”比赛中,各班代表队得分如下(单位:分):9,7,8,7,9,7,6,则各代表队得分的中位数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,以AB为直径作⊙O分别交AC,BC于点D,E,且
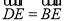

(1)求证:AB=AC.
(2)若∠C=70°,求
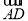 的度数.
的度数.(3)如图2,点F在⊙O上,
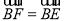 ,连结DF,DE.求证:∠ADF=∠CDE.
,连结DF,DE.求证:∠ADF=∠CDE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式成立的是( )
A.a﹣(b+c)=a﹣b+c
B.a+b﹣c=a+(b﹣c)
C.a+(b+c)=a﹣b+c
D.a+b﹣c=a﹣(b+c) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
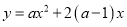 ,其中
,其中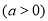 ,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.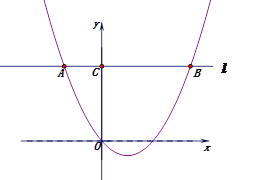
(1)求m的值.
(2)当a=2时,求点B的坐标.
(3)如图2,以OB为对角线作菱形OPBQ,顶点P在直线l上,顶点Q在x轴上.
①若PB=2AP,求a的值.
②菱形OPBQ的面积的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在⊙O上.(不限画图工具,要保留作图痕迹)

(1)作⊙O的内接正三角形ABC.
若⊙O的半径为6,则S扇形OAB=____ ____ .
-
科目: 来源: 题型:
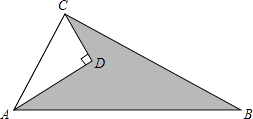
查看答案和解析>>【题目】已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分的面积.
相关试题

