【题目】如图1,在△ABC中,以AB为直径作⊙O分别交AC,BC于点D,E,且![]()

(1)求证:AB=AC.
(2)若∠C=70°,求![]() 的度数.
的度数.
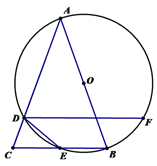
(3)如图2,点F在⊙O上, ![]() ,连结DF,DE.求证:∠ADF=∠CDE.
,连结DF,DE.求证:∠ADF=∠CDE.

参考答案:
【答案】(1)证明见解析(2)100°(3)证明见解析
【解析】(1)连接AE,由圆周角定理得∠AEB=90°,再证⊿AEC≌⊿AEB即可得出AC=AB;(2)利用两弧的差即可求得弧AD![]() 的度数;(3) 利用等弧所对的圆周角相等,圆内接四边形的性质即可求得.
的度数;(3) 利用等弧所对的圆周角相等,圆内接四边形的性质即可求得.
解:(1)连结AE,
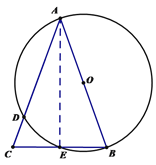
∵AB是直径,
∴∠AEB=900=∠AEC ,
∵弧DE=弧EB![]() ,
,
∴∠CAE=∠EAB,
又∵AE=AE,
∴⊿AEC≌⊿AEB,
∴AC=AB.
(2)∵AB=AC,
∴∠B=∠C=700,
∴∠DAB=400,
∴![]() 弧DB=2∠DAB=800 ,
弧DB=2∠DAB=800 ,
又∵AB是直径,
∴弧ADB![]() =1800,
=1800,
∴弧AD= 弧ADB -弧DB ![]() =1000 .
=1000 .
(3)∵弧BF=弧EB![]() ,AB为直径,
,AB为直径,
∴弧ADB=弧AFB=1800,
∴ 弧AF=弧AE, ![]()
∴∠ADF=∠B ,
又∵四边形ABED内接于圆O,
∴∠CDE=∠B,
∴∠ADF=∠CDE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组式中,为同类项的是( )
A.3x2y与﹣3xy2
B.3xy与﹣2yx
C.2x与2x2
D.7xy与7yz -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(﹣3,0),B(0,1),C(m,n).
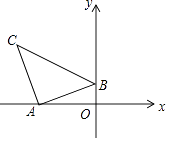
(1)请直接写出C点坐标.
(2)将△ABC沿x轴的正方向平移t个单位,B′、C′两点的对应点、正好落在反比例函数y=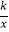 在第一象限内图象上.请求出t,k的值.
在第一象限内图象上.请求出t,k的值.
(3)在(2)的条件下,问是否存x轴上的点M和反比例函数y=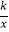 图象上的点N,使得以B′、C′,M,N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′,M,N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级“诗歌大会”比赛中,各班代表队得分如下(单位:分):9,7,8,7,9,7,6,则各代表队得分的中位数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式成立的是( )
A.a﹣(b+c)=a﹣b+c
B.a+b﹣c=a+(b﹣c)
C.a+(b+c)=a﹣b+c
D.a+b﹣c=a﹣(b+c) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )

A.2
B.2
C.4
D.4 -
科目: 来源: 题型:
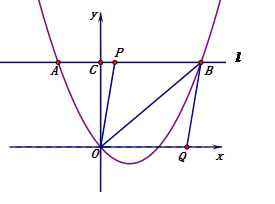
查看答案和解析>>【题目】如图1,抛物线
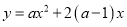 ,其中
,其中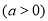 ,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.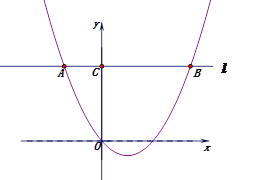
(1)求m的值.
(2)当a=2时,求点B的坐标.
(3)如图2,以OB为对角线作菱形OPBQ,顶点P在直线l上,顶点Q在x轴上.
①若PB=2AP,求a的值.
②菱形OPBQ的面积的最小值是 .
相关试题

