【题目】设函数f(x)= ![]() ﹣ax,e为自然对数的底数 (Ⅰ)若函数f(x)的图象在点(e2 , f(e2))处的切线方程为 3x+4y﹣e2=0,求实数a,b的值;
﹣ax,e为自然对数的底数 (Ⅰ)若函数f(x)的图象在点(e2 , f(e2))处的切线方程为 3x+4y﹣e2=0,求实数a,b的值;
(Ⅱ)当b=1时,若存在 x1 , x2∈[e,e2],使 f(x1)≤f′(x2)+a成立,求实数a的最小值.
参考答案:
【答案】解:(I) ![]() ﹣a(x>0,且x≠1), ∵函数f(x)的图象在点(e2 , f(e2))处的切线方程为 3x+4y﹣e2=0,
﹣a(x>0,且x≠1), ∵函数f(x)的图象在点(e2 , f(e2))处的切线方程为 3x+4y﹣e2=0,
∴f′(e2)= ![]() ﹣a=
﹣a= ![]() ,f(e2)=
,f(e2)= ![]() =﹣
=﹣ ![]() ,
,
联立解得a=b=1.
(II)当b=1时,f(x)= ![]() ,f′(x)=
,f′(x)= ![]() ,
,
∵x∈[e,e2],∴lnx∈[1,2], ![]() .
.
∴f′(x)+a= ![]() =﹣
=﹣ ![]() +
+ ![]() ,
,
∴[f′(x)+a]max= ![]() ,x∈[e,e2].
,x∈[e,e2].
存在 x1 , x2∈[e,e2],使 f(x1)≤f′(x2)+a成立x∈[e,e2],f(x)min≤f(x)max+a= ![]() ,
,
①当a ![]() 时,f′(x)≤0,f(x)在x∈[e,e2]上为减函数,则f(x)min=
时,f′(x)≤0,f(x)在x∈[e,e2]上为减函数,则f(x)min= ![]() ,解得a≥
,解得a≥ ![]() .
.
②当a ![]() 时,由f′(x)=
时,由f′(x)= ![]() ﹣a在[e,e2]上的值域为
﹣a在[e,e2]上的值域为 ![]() .
.
(i)当﹣a≥0即a≤0时,f′(x)≥0在x∈[e,e2]上恒成立,因此f(x)在x∈[e,e2]上为增函数,
∴f(x)min=f(e)= ![]() ,不合题意,舍去.
,不合题意,舍去.
(ii)当﹣a<0时,即 ![]() 时,由f′(x)的单调性和值域可知:存在唯一x0∈(e,e2),使得f′(x0)=0,
时,由f′(x)的单调性和值域可知:存在唯一x0∈(e,e2),使得f′(x0)=0,
且满足当x∈[e,x0),f′(x)<0,f(x)为减函数;当x∈ ![]() 时,f′(x)>0,f(x)为增函数.
时,f′(x)>0,f(x)为增函数.
∴f(x)min=f(x0)= ![]() ﹣ax0
﹣ax0![]() ,x0∈(e,e2).
,x0∈(e,e2).
∴a≥ ![]() ,与
,与 ![]() 矛盾.
矛盾.
(或构造函数 ![]() 即可).
即可).
综上可得:a的最小值为 ![]()
【解析】(I) ![]() ﹣a(x>0,且x≠1),由题意可得f′(e2)=
﹣a(x>0,且x≠1),由题意可得f′(e2)= ![]() ﹣a=
﹣a= ![]() ,f(e2)=
,f(e2)= ![]() =﹣
=﹣ ![]() ,联立解得即可.(II)当b=1时,f(x)=
,联立解得即可.(II)当b=1时,f(x)= ![]() ,f′(x)=
,f′(x)= ![]() ,由x∈[e,e2],可得
,由x∈[e,e2],可得 ![]() .由f′(x)+a=
.由f′(x)+a= ![]() =﹣
=﹣ ![]() +
+ ![]() ,可得[f′(x)+a]max=
,可得[f′(x)+a]max= ![]() ,x∈[e,e2].存在 x1 , x2∈[e,e2],使 f(x1)≤f′(x2)+a成立x∈[e,e2],f(x)min≤f(x)max+a=
,x∈[e,e2].存在 x1 , x2∈[e,e2],使 f(x1)≤f′(x2)+a成立x∈[e,e2],f(x)min≤f(x)max+a= ![]() ,对a分类讨论解出即可.
,对a分类讨论解出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设F为抛物线y2=4x的焦点,A,B,C为该抛物线上不同的三点,
 +
+ 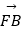 +
+  =
= 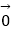 ,O为坐标原点,且△OFA、△OFB、△OFC的面积分别为S1、S2、S3 , 则S12+S22+S32=( )
,O为坐标原点,且△OFA、△OFB、△OFC的面积分别为S1、S2、S3 , 则S12+S22+S32=( )
A.2
B.3
C.6
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】现有四个函数:①y=xsinx;②y=xcosx;③y=x|cosx|;④y=x2x的图象(部分)如图:

则按照从左到右图象对应的函数序号安排正确的一组是( )
A.①④③②
B.③④②①
C.④①②③
D.①④②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人投掷飞镖,他们的成绩(环数)如下面的频数条统计图所示.则甲、乙、丙三人的训练成绩方差S甲2 , S乙2 , S丙2的大小关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两动圆F1:(x+
 )2+y2=r2和F2:(x﹣
)2+y2=r2和F2:(x﹣  )2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足:
)2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足: 
 =0.
=0.
(1)求曲线C的方程;
(2)证明直线AB恒经过一定点,并求此定点的坐标;
(3)求△ABM面积S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?非读书迷
读书迷
合计
男
15
女
45
合计
(2)将频率视为概率,现在从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书谜”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方程D(X) 附:K2= n=a+b+c+d
n=a+b+c+dP(K2≥k0)
0.100
0.050
0.025
0.010
0.001
k0
2.706
3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).

(Ⅰ)求证:PB⊥DE;
(Ⅱ)若PE⊥BE,直线PD与平面PBC所成的角为30°,求PE长.
相关试题

