【题目】如图,在![]() 中,
中,![]() ,高
,高![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则图中共有______________________组全等三角形.
,则图中共有______________________组全等三角形.

参考答案:
【答案】7
【解析】
根据三角形全等的判定法则确定三角形全等,最后统计即可.
解:①△BDC≌△CEB,根据等边对等角得:∠ABC=∠ACB,由高得:∠BDC=∠CEB=90°,所以利用AAS可证明全等;
②△BEO≌△CDO,加上对顶角相等,利用AAS可证明全等;
③△AEO≌△ADO,根据HL可证明全等;
④△ABF≌△ACF,根据SAS可证明全等;
⑤△BOF≌△COF,根据等腰三角形三线合一的性质得:BF=FC,∠AFB=∠AFC,利用SAS可证明全等;
⑥△AOB≌△AOC,根据SAS可证明全等;
⑦△ABD≌△ACE,利用AAS可证明全等.
故答案为:7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F是四边形ABCD对角线AC上的两点,AD∥BC,DF∥BE,AE=CF.
求证:(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月22日是世界地球日,为了增强学生环保意识,某中学八年级举行了“环保知识竞赛”活动,为了了解本次竞赛情况,只抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,请你根据下面还未完成的频数分布表和频数分布直方图,解答下列问题:
分组
频数
频率
50.5~60.5
4
0.08
60.5~70.5
8
0.16
70.5~80.5
10
0.20
80.5~90.5
16
0.32
90.5~100.5
a
b

(1)a= b= ;
(2)补全频数分布直方图;
(3)该校八年级有500名学生,估计八年级学生中竞赛成绩高于80分的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,已知点
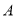 的坐标是
的坐标是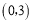 ,点
,点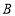 的坐标是
的坐标是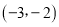
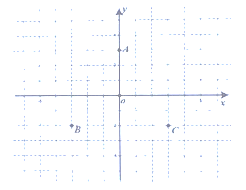
(1)图中点
 的坐标是__________________;
的坐标是__________________;(2)三角形
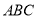 的面积为___________________;
的面积为___________________;(3)点
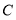 关于
关于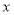 轴对称的点
轴对称的点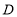 的坐标是______________;
的坐标是______________;(4)如果将点
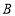 沿着
沿着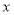 轴平行的方向向右平移3个单位得到点
轴平行的方向向右平移3个单位得到点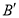 ,那么
,那么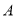 、
、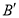 两点之间的距离是_________;
两点之间的距离是_________;(5)图中四边形
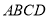 的面积是___________.
的面积是___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,
, 为
为 边的中点,
边的中点,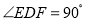 ,
, 绕
绕 点旋转,它的两边分别交
点旋转,它的两边分别交 和
和 (或它们的延长线)于
(或它们的延长线)于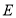 ,
, .
.
(1)当
 于
于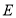 时(如图1),可得
时(如图1),可得 ______________
______________ .
.(2)当
 与
与 不垂直时(如图2),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出
不垂直时(如图2),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出 ,
, ,
, 的关系.
的关系.(3)当点
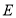 在
在 延长线上时(如图3),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出
延长线上时(如图3),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出 ,
, ,
, 的关系.
的关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
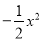 +bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.

相关试题

