搜索
【题目】如图，E，F是四边形ABCD对角线AC上的两点，AD∥BC，DF∥BE，AE=CF．
求证：（1）△AFD≌△CEB；
（2）四边形ABCD是平行四边形．
参考答案：
【答案】（1）证明见解析；（2）证明见解析.
【解析】
（1）根据全等三角形的判定定理ASA证得△AFD≌△CEB；
（2）利用（1）中的全等三角形的对应边相等得到AD=CB，则由“有一组对边相等且平行的四边形是平行四边形”证得结论．
证明：（1）如图，
∵AD∥BC，DF∥BE，∴∠1=∠2，∠3=∠4．
又AE=CF，∴AE+EF=CF+EF，即AF=CE．
在△AFD与△CEB中，
，
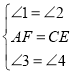∴△AFD≌△CEB（ASA）；
（2）由（1）知，△AFD≌△CEB，则AD=CB．
又∵AD∥BC，
∴四边形ABCD是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】矩形纸片ABCD，AD=4，AB=3，如果点E在边BC上，将纸片沿AE折叠，使点B落在点F处，联结FC，当△EFC是直角三角形时，那么BE的长为____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）作△ABC的外接圆；
（2）若AC=BC，AB=8，C到AB的距离是2，求△ABC的外接圆半径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两同学用一副扑克牌中牌面数字分别是：3，4，5，6的4张牌做抽数学游戏．游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，然后，将所抽的牌放回，正面全部朝下、洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数．若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请运用概率知识说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°， AD是∠BAC的平分线，O是AB上一点, 以OA为半径的⊙O经过点D．
（1）求证：BC是⊙O切线；
（2）若BD=5，DC=3，求AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】4月22日是世界地球日，为了增强学生环保意识，某中学八年级举行了“环保知识竞赛”活动，为了了解本次竞赛情况，只抽取了部分学生的成绩（满分100分，得分均为正整数）进行统计，请你根据下面还未完成的频数分布表和频数分布直方图，解答下列问题：
分组
频数
频率
50.5～60.5
4
0.08
60.5～70.5
8
0.16
70.5～80.5
10
0.20
80.5～90.5
16
0.32
90.5～100.5
a
b
（1）a＝ b＝ ；
（2）补全频数分布直方图；
（3）该校八年级有500名学生，估计八年级学生中竞赛成绩高于80分的有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
，高
，
交于点
，连接
并延长交
于点
，则图中共有______________________组全等三角形．
相关试题
