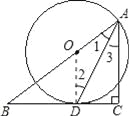
【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
参考答案:
【答案】(1)证明见解析;(2)6.
【解析】试题分析:(1)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可.
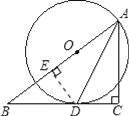
(2)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
试题解析:(1)证明:连接OD;
∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC.
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
(2)解:过点D作DE⊥AB,
∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得: ![]() ,
,
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴![]() .
.
∴![]() .
.
∴AC=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣2)(x+3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=﹣6
B.a=5,b=6
C.a=1,b=6
D.a=1,b=﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁从数轴上一点A 出发,爬了7个单位长度到了原点,则点A所表示的数是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三张正面分别标有数字:
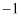 ,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标
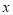 ,第二次抽出的数字作为点的纵坐标
,第二次抽出的数字作为点的纵坐标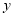 ,求点(
,求点(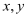 )落在双曲线上
)落在双曲线上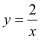 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC,BD交于点O,已知O是BD的中点,BE=DF,AF∥CE.
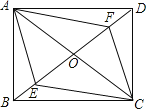
(1)求证:四边形AECF是平行四边形;
(2)若OA=OD,则四边形ABCD是什么特殊四边形?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
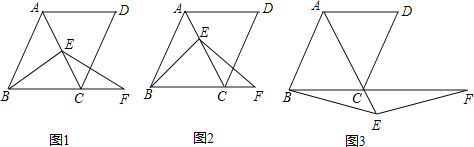
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.
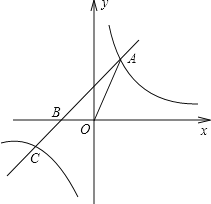
(1)求双曲线的解析式;
(2)求B点的坐标;
(3)若S△AOB=2,求A点的坐标;
(4)在(3)的条件下,在x轴上是否存在点P,使△AOP是等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
相关试题

