【题目】如图甲,直线PA交O于A、E两点,PA的垂线CD切O于点C,过点A作O的直径AB.
(1)求证:AC平分∠DAB;
(2)将直线CD向下平行移动,在将直线CD向下平行移动的过程中,如图乙、丙,试指出与∠DAC相等的角(不要求证明).
(3)在图甲中,若DC+DA=6,O的直径为10,求AE的长度.
参考答案:
【答案】
(1)
证明:如图1,连接OC,
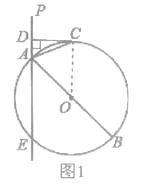
∵OA、OC是O的半径,
∴ OA=OC.
∴ ∠OAC=∠OCA,
∵CD切于圆O于点C,
∴ CD⊥OC,
又∵CD⊥PA,
∴ OC//PA,
∴ ∠PAC=∠OCA,
∴ ∠OAC=∠PAC,
∴ AC平分∠DAB.
(2)
∠DAC=∠BAF,理由如下:
如图2,连接BC,
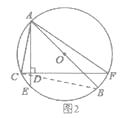
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACF+∠BCF=90°,
又∵在Rt△ACD中,∠DAC+∠ACD=90°,
∴∠DAC=∠FCB,
又∵∠BAF =∠FCB,
∴∠DAC=∠BAF.
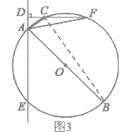
如图3,∵AB是圆O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
又∵∠DAF+∠AFD=90°,∠AFD =∠CBA,
∴∠DAF=∠CAB,
∴∠DAF-∠CAF=∠CAB-∠CAF.
∴∠DAC=∠BAF.
(3)
解:如图4所示:连接OC,过点A作AF⊥CO,垂足为F,连接CB、CE.
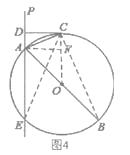
∵DC垂直AE,OC垂直DC,AF垂直CO,
∴ 四边形AFCD为矩形.
∴ DC=AF,AD=CF.
设AD的长为x,则AF=6-x,OF=5-x.
在Rt△AFO中,OA2=AF2+OF2,即:25=(6-x)2+(5-x)2,
解得:x1=2,x2=9(舍去).
∴ AD=2,DC=4.
由(1)可知:∠DAC=∠BAC,
又∵∠CAD+∠DCA=90°,∠CAB+∠ABC=90°,
∴ ∠DCA=∠ABC,
∵∠DEC=∠ABC,
∴ ∠DEC=∠DCA,
又∵∠EDC=∠ADC,
∴ △EDC~△CDA,
∴ ![]() ,即:
,即: ![]() ,
,
∴ DE=8,
∴ AE=DE-AD=8-2=6.
【解析】(1)需要证明∠OAC=∠PAC,连接OC,则OC=OA,则∠OAC=∠OCA,所以需要证明∠PAC=∠OCA,则需要证明AD//OC,而CD⊥PA,则CD⊥OC,由CD切于圆O于点C,可证得;(2)如图2,根据两角和为90°,等量代换得到∠DAC=∠FCB,由同弧所对的圆周角相等可得∠BAF =∠FCB,从而证得∠DAC=∠BAF;如图3,同理由两角和为90°,等量代换得到∠DAF=∠CAB,则∠DAC=∠BAF.(3)连接OC,过点A作AF⊥CO,垂足为F,连接CB、CE,则易得DC=AF,AD=CF,可设AD的长为x,则AF=6-x,OF=5-x,在Rt△AFO中,由勾股定理构造方程解出x,由(1)和(2)可证得∠DEC=∠DCA,又∠EDC=∠ADC,则△EDC~△CDA,由对应边成比例解出DE,则AE=DE-AD.
【考点精析】认真审题,首先需要了解圆的定义(平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2=
 GF×AF;④当AG=6,EG=2
GF×AF;④当AG=6,EG=2 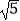 时,BE的长为
时,BE的长为 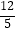
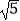 ,其中正确的结论个数是( )
,其中正确的结论个数是( ) 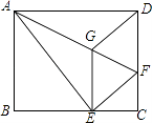
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60度,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45度,已知山坡AB的坡度i=1:
 ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某工程,乙工程队单独先做10天后,再由甲,乙两个工程队合作20天就能完成全部工程,已知甲工程队单独完成此工程所需天数是乙工程队单独完成此工程所需天数的
 ,
,
(1)求:甲,乙工程队单独做完成此工程各需多少天?
(2)甲工程队每天的费用为0.67万元,乙工程队每天的费用为0.33万元,该工程的预算费用为20万元,若甲,乙工程队一起合作完成该工程,请问工程费用是否够用,若不够用应追加多少万元? -
科目: 来源: 题型:
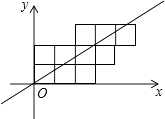
查看答案和解析>>【题目】如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
 与二次函数
与二次函数  在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
A.
B.
C.
D.
相关试题

