【题目】一次函数 ![]() 与二次函数
与二次函数 ![]() 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
A.
B.
C.
D.
参考答案:
【答案】C
【解析】A.由一次函数 y = ax + b 的图象可得: a > 0 , b > 0 ,此时二次函数 y = ax2 + bx + c 的图象应该开口向上,故 A 错误;
B.由一次函数 y = ax + b 的图象可得: a > 0 , b > 0 ,此时二次函数 y = ax2+ bx + c 的图象应该开口向上,对称轴 x= ![]() < 0,故B错误;
< 0,故B错误;
C.由一次函数 y = ax + b 的图象可得: a < 0 , b < 0 ,此时二次函数 y = ax2 + bx + c 的图象应该开口向下,对称轴 x= ![]() < 0,故C正确;
< 0,故C正确;
D.由一次函数 y = ax + b 的图象可得: a < 0 , b > 0 ,此时二次函数 y = ax2+ bx + c 的图象应该开口向下,对称轴 x= ![]() > 0 ,故 D 错误.
> 0 ,故 D 错误.
故选C.
【考点精析】关于本题考查的一次函数的图象和性质和二次函数的图象,需要了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,直线PA交O于A、E两点,PA的垂线CD切O于点C,过点A作O的直径AB.

(1)求证:AC平分∠DAB;
(2)将直线CD向下平行移动,在将直线CD向下平行移动的过程中,如图乙、丙,试指出与∠DAC相等的角(不要求证明).
(3)在图甲中,若DC+DA=6,O的直径为10,求AE的长度. -
科目: 来源: 题型:
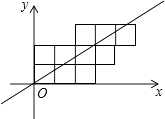
查看答案和解析>>【题目】如图,10个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这10个正方形分成面积相等的两部分,则该直线l的解析式为
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a,b,c分别为
 三边的长.
三边的长.
(1)如果 是方程的根,则
是方程的根,则  的形状为 ;
的形状为 ;
(2)如果方程有两个相等的实数根,试判断 的形状,并说明理由;
的形状,并说明理由;
(3)如果 是等边三角形,试求这个一元二次方程的根.
是等边三角形,试求这个一元二次方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线


(1)此抛物线的顶点坐标是 ,与x轴的交点坐标是 , ,与y轴交点坐标是 ,对称轴直线是 ;
(2)在平面直角坐标系中画出 的图象;
的图象;
(3)结合图象,说明当x取何值时,y随x的增大而减小.
相关试题

