【题目】某商场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的距离CD=2.8米,一楼到地平线的距离BC=1米.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1米)
(2)如果给该商场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)

参考答案:
【答案】(1)5.6米;(2)能,理由见解析
【解析】(1)由题意可得∠BAD=18°,BD=CD-CB=1.8(米),然后在Rt△ABD中,由三角函数的性质,即可求得AB的长;
(2)首先过C作CE⊥AD,垂足为E,可求得∠DCE的度数,然后在Rt△CDE中,由三角函数的性质即可得CE=CDcos18°,继而求得答案.
解:(1)由题意可得∠BAD=18°.在Rt△ABD中,AB=![]() ≈
≈![]() ≈5.6(米)
≈5.6(米)
答:应在地面上距B点5.6米远的A处开始斜坡的施工
(2)能.理由:如图,过点C作CE⊥AD于点E,
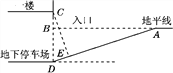
则∠DCE=∠BAD=18°.在Rt△CED中,CE=CD·cos 18°≈2.8×0.95=2.66(米).
∵2.66>2.5,
∴能保证货车顺利进入地下停车场.
-
科目: 来源: 题型:
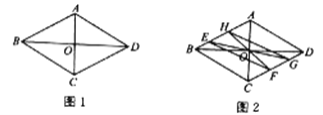
查看答案和解析>>【题目】如图1,点
 是菱形
是菱形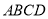 对角线的交点,已知菱形的边长为12,
对角线的交点,已知菱形的边长为12,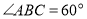 .
.
(1)求
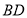 的长;
的长;(2)如图2,点
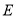 是菱形边上的动点,连结
是菱形边上的动点,连结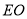 并延长交对边于点
并延长交对边于点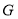 ,将射线
,将射线 绕点
绕点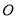 顺时针旋转
顺时针旋转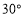 交菱形于点
交菱形于点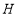 ,延长
,延长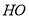 交对边于点
交对边于点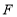 .
.①求证:四边形
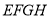 是平行四边形;
是平行四边形;②若动点
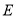 从点
从点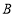 出发,以每秒1个单位长度沿
出发,以每秒1个单位长度沿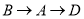 的方向在
的方向在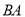 和
和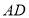 上运动,设点
上运动,设点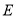 运动的时间为
运动的时间为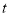 ,当
,当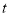 为何值时,四边形
为何值时,四边形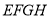 为矩形.
为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点G,E、F分别是边AD、BC的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( )
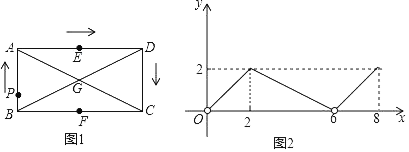
A. 点CB. 点EC. 点FD. 点G
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,有下列条件:①AB
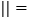 CD;②AD
CD;②AD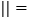 BC;③AC=BD;④AC⊥BD.
BC;③AC=BD;④AC⊥BD.(1)从中任选一个作为已知条件,能判定四边形ABCD是平行四边形的概率是 .
(2)从中任选两个作为已知条件,请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率,并判断四边形ABCD是菱形的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四边形ABCD中,AD//BC,对角线AC、BD交于点O,且AC=BD,下列四个命题中真命题是( )
A. 若AB=CD,则四边形ABCD一定是等腰梯形;
B. 若∠DBC=∠ACB,则四边形ABCD一定是等腰梯形;
C. 若
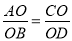 ,则四边形ABCD一定是矩形;
,则四边形ABCD一定是矩形;D. 若AC⊥BD且AO=OD,则四边形ABCD一定是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形
 是半高三角形,且斜边
是半高三角形,且斜边 ,则它的周长等于_________.
,则它的周长等于_________.
相关试题

