【题目】如图1,点![]() 是菱形
是菱形![]() 对角线的交点,已知菱形的边长为12,
对角线的交点,已知菱形的边长为12,![]() .
.
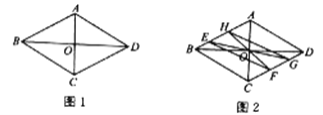
(1)求![]() 的长;
的长;
(2)如图2,点![]() 是菱形边上的动点,连结
是菱形边上的动点,连结![]() 并延长交对边于点
并延长交对边于点![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交菱形于点
交菱形于点![]() ,延长
,延长![]() 交对边于点
交对边于点![]() .
.
①求证:四边形![]() 是平行四边形;
是平行四边形;
②若动点![]() 从点
从点![]() 出发,以每秒1个单位长度沿
出发,以每秒1个单位长度沿![]() 的方向在
的方向在![]() 和
和![]() 上运动,设点
上运动,设点![]() 运动的时间为
运动的时间为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 为矩形.
为矩形.
参考答案:
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)解直角三角形求出BO即可解决问题;
(2)①想办法证明OE=OG,HO=FO即可解决问题;
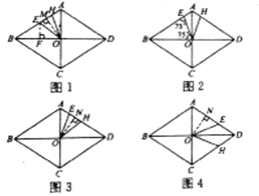
②分四种情形画出图形,(Ⅰ)如图1,当![]() 时,
时,![]() ,
,![]() 关于
关于![]() 对称,(Ⅱ)如图2,当
对称,(Ⅱ)如图2,当![]() ,
,![]() 关于
关于![]() 对称时,
对称时,![]() ,(Ⅲ)如图3,此时
,(Ⅲ)如图3,此时![]() 与图2中的
与图2中的![]() 的位置相同,(Ⅳ)如图4,当
的位置相同,(Ⅳ)如图4,当![]() ,
,![]() 关于
关于![]() 对称时,四边形EFGH是矩形.分别求解即可解决问题;
对称时,四边形EFGH是矩形.分别求解即可解决问题;
解:(1)∵四边形![]() 为菱形,
为菱形,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①∵四边形ABCD是菱形,
∴AB∥CD,BO=OD,
∴∠EBO=∠GDO
∵∠BOE=∠DOG,
∴△EOB≌△GOD,
∴EO=GO,同理可得HO=FO,
∴四边形EFGH是平行四边形.
②由①得四边形![]() 为平行四边形,
为平行四边形,
∴当![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
(Ⅰ)如图1,当![]() 时,
时,![]() ,
,![]() 关于
关于![]() 对称.
对称.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
过点![]() 作
作![]() 于
于![]() 点,
点,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ,
,
∴![]() ,
,
∴![]() ;
;
(Ⅱ)如图2,当![]() ,
,![]() 关于
关于![]() 对称时,
对称时,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ;
;
(Ⅲ)如图3,此时![]() 与图2中的
与图2中的![]() 的位置相同,
的位置相同,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(Ⅳ)如图4,当![]() ,
,![]() 关于
关于![]() 对称时,
对称时,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
综上所述,![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛.同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.请你根据图中所给信息解答下列问题:
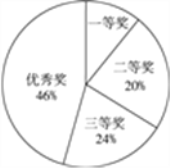

(1)一等奖所占的百分比是__________.
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整.
(3)各奖项获奖学生分别有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的标价为500元/件,经过两次降价后的价格为320元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该商品进价为280元/件,两次降价共售此种商品100件,为使两次降价销售的总利润不少于8000元,则第一次降价后至少要售出这种商品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(新知理解)
如图1,点
 在线段
在线段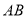 上,点
上,点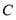 将线段
将线段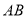 分成两条不相等的线段
分成两条不相等的线段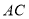 ,
,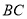 ,如果较长线段
,如果较长线段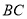 是较短线段
是较短线段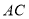 的
的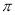 倍,即
倍,即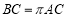 ,则称点
,则称点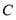 是线段
是线段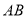 的一个圆周率点,此时,线段
的一个圆周率点,此时,线段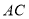 ,
,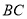 称为互为圆周率伴侣线段.由此可知,一条线段
称为互为圆周率伴侣线段.由此可知,一条线段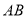 的圆周率点有两个,一个在线段
的圆周率点有两个,一个在线段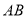 中点的左侧(如图中点
中点的左侧(如图中点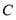 ),另一个在线段
),另一个在线段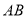 中点的右侧.
中点的右侧.
(1)如图1,若
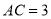 ,则
,则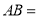 ;若点
;若点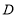 是线段
是线段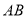 的不同于点
的不同于点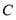 的圆周率点,则
的圆周率点,则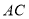
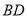 (填“
(填“ ”或“
”或“ ”);
”);(2)如果线段
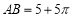 ,点
,点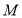 是线段
是线段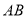 的圆周率点,则
的圆周率点,则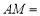 ;
;(问题探究)
(3)如图2,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动的滚动一周,该点到达点
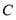 的位置.若点
的位置.若点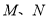 是线段
是线段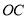 的两个不同的圆周率点,求线段
的两个不同的圆周率点,求线段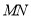 的长;
的长;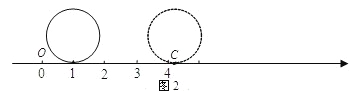
(问题解决)
(4)如图3,将直径为1个单位长度的圆片上的某点与数轴上表示2的点重合,并把圆片沿数轴向右无滑动的滚动一周,该点到达点
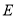 的位置.若点
的位置.若点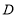 在射线
在射线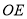 上,且线段
上,且线段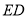 与以
与以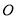 、
、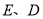 中某两个点为端点的线段互为圆周率伴侣线段,请你直接写出点
中某两个点为端点的线段互为圆周率伴侣线段,请你直接写出点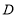 所表示的数.
所表示的数.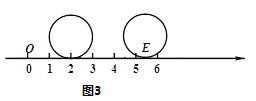
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点G,E、F分别是边AD、BC的中点,AB=2,BC=4,一动点P从点B出发,沿着B﹣A﹣D﹣C的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( )
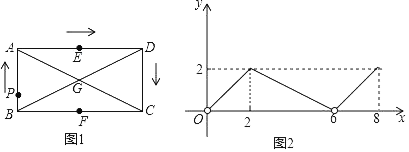
A. 点CB. 点EC. 点FD. 点G
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,有下列条件:①AB
 CD;②AD
CD;②AD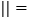 BC;③AC=BD;④AC⊥BD.
BC;③AC=BD;④AC⊥BD.(1)从中任选一个作为已知条件,能判定四边形ABCD是平行四边形的概率是 .
(2)从中任选两个作为已知条件,请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率,并判断四边形ABCD是菱形的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的距离CD=2.8米,一楼到地平线的距离BC=1米.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1米)
(2)如果给该商场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)

相关试题

