【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

参考答案:
【答案】(1))AB是⊙O切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)结论:AB是⊙O切线,连接DE,CF,由∠FCD+∠CDF=90°,只要证明∠ADF=∠DCF即可解决问题.
(2)只要证明△PCF∽△PAC,得![]() ,设PF=a.则PC=2a,列出方程即可解决问题.
,设PF=a.则PC=2a,列出方程即可解决问题.
试题解析:(1)AB是⊙O切线.
理由:连接DE、CF.

∵CD是直径,
∴∠DEC=∠DFC=90°,
∵∠ACB=90°,
∴∠DEC+∠ACE=180°,
∴DE∥AC,
∴∠DEA=∠EAC=∠DCF,
∵∠DFC=90°,
∴∠FCD+∠CDF=90°,
∵∠ADF=∠EAC=∠DCF,
∴∠ADF+∠CDF=90°,
∴∠ADC=90°,
∴CD⊥AD,
∴AB是⊙O切线.
(2)∵∠CPF=∠CPA,∠PCF=∠PAC,
∴△PCF∽△PAC,
∴![]() ,
,
∴PC2=PFPA,设PF=a.则PC=2a,
∴4a2=a(a+5),
∴a=![]() ,
,
∴PC=2a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和等于1260°,则这个多边形是_____边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的顶角为80°,则它的一个底角为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果收入80元记作+80 元,那么支出20元记作________________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)
(1) 描出A、B、C、D、四点的位置,并顺次连接ABCD,
(2) 四边形ABCD的面积是________.
(3) 把四边形ABCD向左平移5个单位,再向下平移2个单位得到四边形A'B'C'D',写出点A'、B'、C'、D'的坐标.
-
科目: 来源: 题型:
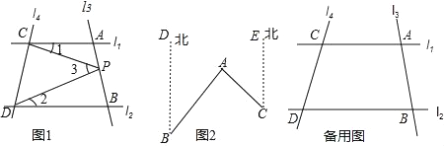
查看答案和解析>>【题目】探索发现:如图1,已知直线l1∥l2,且l3和l1、l2分别相交于A、B两点,l4和l1、l2分别交于C、D两点,∠ACP记作∠1,∠BDP记作∠2,∠CPD记作∠3.点P在线段AB上.
(1)若∠1=20°,∠2=30°,请你求出∠3的度数
归纳总结:(2)请你根据上述问题,请你找出图1中∠1、∠2、∠3之间的数量关系,并直接写出你的结论.
实践应用:(3)应用(2)中的结论解答下列问题:如图2,点A在B的北偏东40°的方向上,在C的北偏西45°的方向上,请你根据上述结论直接写出∠BAC的度数.
拓展延伸:(4)如果点P在直线l3上且在A、B两点外侧运动时,其他条件不变,试探究∠1、∠2、
∠3之间的关系(点P和A、B两点不重合),写出你的结论并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( ).

A.①②③ B.①③④ C.①②④ D.①②③④
相关试题

