【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形![]() 是半高三角形,且斜边
是半高三角形,且斜边![]() ,则它的周长等于_________.
,则它的周长等于_________.
参考答案:
【答案】5+3![]() 或5+5
或5+5![]()
【解析】由题意可知,存在以下两种情况:
(1)当一条直角边是另一条直角边的一半时,这个直角三角形是半高三角形,此时设较短的直角边为a,则较长的直角边为2a,由勾股定理可得:
![]() ,解得:
,解得: ![]() ,
,
∴此时较短的直角边为![]() ,较长的直角边为
,较长的直角边为![]() ,
,
∴此时直角三角形的周长为: ![]() ;
;
(2)当斜边上的高是斜边的一半是,这个直角三角形是半高三角形,此时设两直角边分别为x、y,
这有题意可得:①![]() ,②S△=
,②S△=![]() ,
,
∴③![]() ,
,
由①+③得: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴此时这个直角三角形的周长为: ![]() .
.
综上所述,这个半高直角三角形的周长为: ![]() 或
或![]() .
.
故答案为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问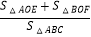 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4.
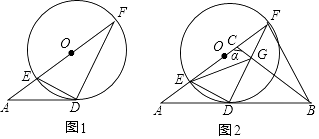
(1)证明:AD2=AEAF;
(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB交DF于点G,连接EG,设∠ACB=α,BG=x,EG=y. ①当α=900时,探索EG与BD的大小关系?并说明理由;
②当α=1200时,求y与x的关系式,并用x的代数式表示y. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=
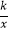 (k>0)上,则k的值为( )
(k>0)上,则k的值为( )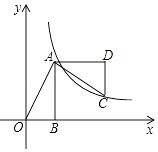
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
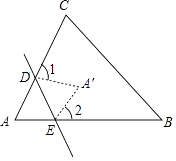
查看答案和解析>>【题目】如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
A.α
B.2α
C.180°﹣α
D.180°﹣2α -
科目: 来源: 题型:
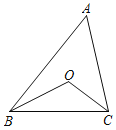
查看答案和解析>>【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列4个结论::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④点M(x1 , y1)、N(x2 , y2)在抛物线上,若x1<x2 , 则y1≤y2 , 其中正确结论的个数是( )
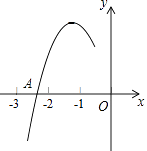
A.1个
B.2个
C.3个
D.4个
相关试题

