【题目】已知在四边形ABCD中,AD//BC,对角线AC、BD交于点O,且AC=BD,下列四个命题中真命题是( )
A. 若AB=CD,则四边形ABCD一定是等腰梯形;
B. 若∠DBC=∠ACB,则四边形ABCD一定是等腰梯形;
C. 若![]() ,则四边形ABCD一定是矩形;
,则四边形ABCD一定是矩形;
D. 若AC⊥BD且AO=OD,则四边形ABCD一定是正方形.
参考答案:
【答案】C
【解析】A、因为满足本选项条件的四边形ABCD有可能是矩形,因此A中命题不一定成立;
B、因为满足本选项条件的四边形ABCD有可能是矩形,因此B中命题不一定成立;
C、因为由![]() 结合AO+CO=AC=BD=BO+OD可证得AO=CO,BO=DO,由此即可证得此时四边形ABCD是矩形,因此C中命题一定成立;
结合AO+CO=AC=BD=BO+OD可证得AO=CO,BO=DO,由此即可证得此时四边形ABCD是矩形,因此C中命题一定成立;
D、因为满足本选项条件的四边形ABCD有可能是等腰梯形,由此D中命题不一定成立.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,有下列条件:①AB
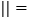 CD;②AD
CD;②AD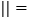 BC;③AC=BD;④AC⊥BD.
BC;③AC=BD;④AC⊥BD.(1)从中任选一个作为已知条件,能判定四边形ABCD是平行四边形的概率是 .
(2)从中任选两个作为已知条件,请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率,并判断四边形ABCD是菱形的概率?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的距离CD=2.8米,一楼到地平线的距离BC=1米.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1米)
(2)如果给该商场送货的货车高度为2.5米,那么按这样的设计能否保证货车顺利进入地下停车场?请说明理由.(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形
 是半高三角形,且斜边
是半高三角形,且斜边 ,则它的周长等于_________.
,则它的周长等于_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的长为1,点P是线段BD上的一点,联结CP,将△BCP沿着直线CP翻折,若点B落在边AD上的点E处,且EP//AB,则AB的长等于________.
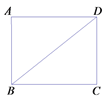
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,点D在BA的延长线上,BC=24,
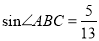 .
.(1)求AB的长;
(2)若AD=6.5,求
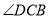 的余切值.
的余切值.
相关试题

