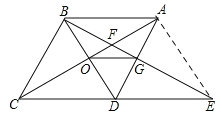
【题目】如图,菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于
交于![]() ,
,![]() 为
为![]() 延长线上的一点,且
延长线上的一点,且![]() ,连结
,连结![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() 则下列结论:①
则下列结论:①![]() ;②与
;②与![]() 全等的三角形共有
全等的三角形共有![]() 个;③
个;③![]() ;④由点
;④由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形是菱形.其中正确的是( )
构成的四边形是菱形.其中正确的是( )

A.①④B.①③④C.①②③D.②③④
参考答案:
【答案】A
【解析】
连结![]() ,可说明四边形
,可说明四边形![]() 是平行四边形,即
是平行四边形,即![]() 是
是![]() 的中点;由有题意的可得O是BD的中点,即可判定①;运用菱形和平行四边形的性质寻找判定全等三角形的条件,找出与其全等的三角形即可判定②;证出OG是△ABD的中位线,得出OG//AB,OG=
的中点;由有题意的可得O是BD的中点,即可判定①;运用菱形和平行四边形的性质寻找判定全等三角形的条件,找出与其全等的三角形即可判定②;证出OG是△ABD的中位线,得出OG//AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形0DGF=S△ABF.即可判定③;先说明△ABD是等边三角形,则BD=AB,即可判定④.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形0DGF=S△ABF.即可判定③;先说明△ABD是等边三角形,则BD=AB,即可判定④.
解:如图:连结![]() .
.
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 是
是![]() 的中点,
的中点,
∵O是BD的中点
![]() ,①正确;
,①正确;
有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 个,②错误;
个,②错误;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG//AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∵△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△A0G的面积=△B0G的面积,
.∴![]() ;不正确;③错误;
;不正确;③错误;
![]()
![]() 是等边三角形.
是等边三角形.
![]() ,
,
![]() 是菱形,④正确.
是菱形,④正确.
故答案为A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°

(1)求tan∠OAB的值;
(2)求图中阴影部分的面积S;
(3)在⊙O上一点P从A点出发,沿逆时针方向运动一周,回到点A,在点P的运动过程中,满足S△POA=S△AOB时,直接写出P点所经过的弧长(不考虑点P与点B重合的情形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理结论及推理说明:
如图,已知∠
 +∠
+∠ =180°,∠
=180°,∠ =∠
=∠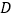 .求证:∠
.求证:∠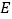 =∠
=∠ .
.证明:∵∠
 +∠
+∠ =180°(已知)
=180°(已知)∴
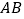 ∥
∥ ( )
( )∴∠
 = ( )
= ( )又∵∠
 =∠
=∠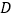 (已知)
(已知)= (等量代换)
∴
 ∥
∥ ( )
( )∴∠
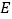 =∠
=∠ ( )
( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,平行四边形
 中,连接
中,连接 ,
, ,过点
,过点 作
作 ,垂足为
,垂足为 ,延长
,延长 与
与 相交于点
相交于点 .
.
(1)如图1,若
 ,
, ,求线段
,求线段 的长;
的长;(2)如图2,若
 ,过点
,过点 作
作 于点
于点 ,连接
,连接 、
、 .求证:
.求证: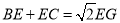 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了
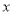 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
学生最喜欢的节目人数条形统计图
节目
人数( 名 )
百分比
最强大脑
5
10%
朗读者
15
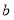 %
%中国诗词大会
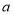
40%
出彩中国人
10
20%
学生最喜爱的节目人数统计表
根据以上提供的信息,解答下列问题:
(1)
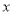 =
= 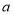 =
= 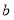 = ;
= ;(2)补全条形统计图;
(3)若该校共有学生1200名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)
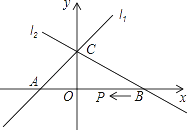
(1)求a、b的值;
(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;
(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

相关试题

