【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)由平行四边形的性质和角平分线易证∠BAE=∠BEA,根据等腰三角形的性质可得AB=BE;(2)易证△ABE是等边三角形,根据等边三角形的性质可得AE=AB=4,AF=EF=2,由勾股定理求出BF,再由AAS证明△ADF≌△ECF,即△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=![]() AEBF,即可得出结果.
AEBF,即可得出结果.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,∴BE=CD;
(2)解:∵AB=BE,∠BEA=60°,
∴△ABE是等边三角形,
∴AE=AB=4,
∵BF⊥AE,
∴AF=EF=2,
∴BF=![]() ,
,
∵AD∥BC,
∴∠D=∠ECF,∠DAF=∠E,
在△ADF和△ECF中,
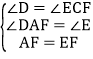 ,
,
∴△ADF≌△ECF(AAS),
∴△ADF的面积=△ECF的面积,
∴平行四边形ABCD的面积=△ABE的面积=![]() AEBF=
AEBF=![]() ×4×2
×4×2![]() =4
=4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我省2014年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展, 2016年的快递业务量达到4.5亿件.设2015年与2016年这两年的平均增长率为x,则下列方程正确的是( )
A. 1.4(1+x)=4.5 B. 1.4(1+2x)=4.5
C. 1.4(1+x)2=4.5 D. 1.4(1+x)+1.4(1+x)2=4.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 (x+3)(x-2)=x2+ax+b , 则a、b的值分别是( )
A.a=-1,b=-6
B.a=1,b=-6
C.a=-1,b=6
D.a=1,b=6 -
科目: 来源: 题型:
查看答案和解析>>【题目】若m是方程x2+x-1=0的根,则2m2+2m+2016的值为( )
A. 2016 B. 2017 C. 2018 D. 2019
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为
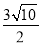 ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.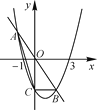
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个样本有50个数据,其中最大值是208,最小值是169,最大值与最小值的差是______;如果取组距为5,那么这组数据应分成______组,第一组的起点为________,第二组与第一组的分点为________.
相关试题

