【题目】已知,如图直线l1的解析式为y=x+1,直线l2的解析式为y=ax+b(a≠0);这两个图象交于y轴上一点C,直线l2与x轴的交点B(2,0)
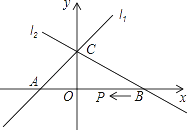
(1)求a、b的值;
(2)过动点Q(n,0)且垂直于x轴的直线与l1、l2分别交于点M、N都位于x轴上方时,求n的取值范围;
(3)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
参考答案:
【答案】(1)a=﹣![]() ;(2)﹣1<n<2;(3)满足条件的时间t为1s,2s,或(3+
;(2)﹣1<n<2;(3)满足条件的时间t为1s,2s,或(3+![]() )或(3﹣
)或(3﹣![]() )s.
)s.
【解析】试题分析:(1)、根据题意求出点C的坐标,然后将点C和点B的坐标代入直线解析式求出a和b的值;(2)、根据题意可知点Q在点A和点B之间,从而求出n的取值范围;(3)、本题需要分几种情况分别来进行计算,即AC=P1C,P2A=P2C和AP3=AC三种情况分别进行计算得出t的值.
试题解析:(1)、解:∵点C是直线l1:y=x+1与轴的交点, ∴C(0,1),
∵点C在直线l2上, ∴b=1, ∴直线l2的解析式为y=ax+1, ∵点B在直线l2上,
∴2a+1=0, ∴a=﹣![]() ;
;
(2)、解:由(1)知,l1的解析式为y=x+1,令y=0, ∴x=﹣1,
由图象知,点Q在点A,B之间, ∴﹣1<n<2
(3)、解:如图,
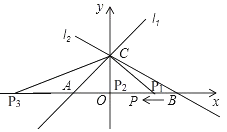
∵△PAC是等腰三角形, ∴①点x轴正半轴上时,当AC=P1C时,
∵CO⊥x轴, ∴OP1=OA=1, ∴BP1=OB﹣OP1=2﹣1=1, ∴1÷1=1s,
②当P2A=P2C时,易知点P2与O重合, ∴BP2=OB=2, ∴2÷1=2s,
③点P在x轴负半轴时,AP3=AC, ∵A(﹣1,0),C(0,1), ∴AC=![]() , ∴AP3=
, ∴AP3=![]() ,
,
∴BP3=OB+OA+AP3=3+![]() 或BP3=OB+OA﹣AP3=3﹣
或BP3=OB+OA﹣AP3=3﹣![]() ,
,
∴(3+![]() )÷1=(3+
)÷1=(3+![]() )s,或(3﹣
)s,或(3﹣![]() )÷1=(3﹣
)÷1=(3﹣![]() )s,
)s,
即:满足条件的时间t为1s,2s,或(3+![]() )或(3﹣
)或(3﹣![]() )s.
)s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,平行四边形
 中,连接
中,连接 ,
, ,过点
,过点 作
作 ,垂足为
,垂足为 ,延长
,延长 与
与 相交于点
相交于点 .
.
(1)如图1,若
 ,
, ,求线段
,求线段 的长;
的长;(2)如图2,若
 ,过点
,过点 作
作 于点
于点 ,连接
,连接 、
、 .求证:
.求证: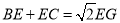 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 中,
中, ,
, 与
与 交于
交于 ,
, 为
为 延长线上的一点,且
延长线上的一点,且 ,连结
,连结 分别交
分别交 ,
, 于点
于点 ,
, ,连结
,连结 则下列结论:①
则下列结论:①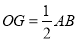 ;②与
;②与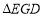 全等的三角形共有
全等的三角形共有 个;③
个;③ ;④由点
;④由点 ,
, ,
, ,
, 构成的四边形是菱形.其中正确的是( )
构成的四边形是菱形.其中正确的是( )
A.①④B.①③④C.①②③D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了
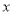 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
学生最喜欢的节目人数条形统计图
节目
人数( 名 )
百分比
最强大脑
5
10%
朗读者
15
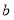 %
%中国诗词大会
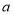
40%
出彩中国人
10
20%
学生最喜爱的节目人数统计表
根据以上提供的信息,解答下列问题:
(1)
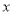 =
= 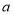 =
= 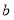 = ;
= ;(2)补全条形统计图;
(3)若该校共有学生1200名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】背景情境:
赛赛同学在学习《一元二次方程》中做过这样一道题:
题目:已知实数
 、
、 满足
满足 ,
, ,且
,且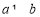 ,求
,求 的值.
的值.解:根据题意得
 与
与 为方程
为方程 的两根,
的两根,∴
 ,
,
∴

请认真阅读赛赛同学解题的方法,仔细思考.
解决问题:
(1)已知实数
 、
、 满足
满足 ,
, ,且
,且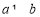 ,求
,求 的值.
的值.(2)设实数
 、
、 分别满足
分别满足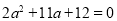 ,
, ,且
,且 ,求
,求 的值.
的值.(3)已知关于
 的方程
的方程 有两个根
有两个根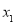 、
、 满足
满足 .当
.当 的三边
的三边 、
、 、
、 满足
满足 ,
, ,
, (a≠b).求
(a≠b).求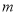 的值以及
的值以及 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
相关试题

