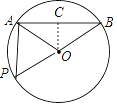
【题目】如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°

(1)求tan∠OAB的值;
(2)求图中阴影部分的面积S;
(3)在⊙O上一点P从A点出发,沿逆时针方向运动一周,回到点A,在点P的运动过程中,满足S△POA=S△AOB时,直接写出P点所经过的弧长(不考虑点P与点B重合的情形).
参考答案:
【答案】(1)![]() ;(2)(
;(2)(![]() π﹣
π﹣![]() )cm2;(3)P点所经过的弧长为
)cm2;(3)P点所经过的弧长为 ![]() πcm或
πcm或![]() πcm或
πcm或![]() πcm.
πcm.
【解析】试题分析:(1)、根据等腰三角形的性质求出∠OAB的角度,从而根据特殊角的三角函数值求出它的值;(2)、阴影部分的面积等于扇形AOB的面积减去△OAB的面积;(3)、本题需要分∠AOP=60°、∠AOP=120°和点P在弧AB上三种情况来分别进行计算,得出答案.
试题解析:(1)、解:∵OA=OB, ∴∠OAB=∠OBA,
∵∠OAB= ![]() (180°﹣120°)=30°, ∴tan∠OAB=tan30°=
(180°﹣120°)=30°, ∴tan∠OAB=tan30°=![]() ;
;
(2)、解:作OC⊥AB于C,如图,则AC=BC,
在Rt△OAC中,OC=![]() OA=1,AC=
OA=1,AC=![]() OC=
OC=![]() , ∴AB=2AC=2
, ∴AB=2AC=2![]() ,
,
∴S弓形AB=S扇形AOB﹣S△AOB=![]() ﹣
﹣![]() 2
2![]() 1=(
1=(![]() π﹣
π﹣![]() )cm2;
)cm2;
(3)、解:延长BO交⊙O于P, ∵OP=OB, ∴此时S△AOP=S△AOB,
∵∠AOP=∠OAB+∠OBA=60°, ∴此时P点所经过的弧长=![]() π(cm);
π(cm);
当点P在弧AB上,且∠AOP=60°时,时S△AOP=S△AOB ,
此时P点所经过的弧长=2π2﹣![]() π=
π=![]() π(cm);
π(cm);
当∠AOP=120时,S△AOP=S△AO, ∴此时P点所经过的弧长=![]() π(cm);
π(cm);
综上所述,P点所经过的弧长为![]() πcm或
πcm或![]() πcm或
πcm或![]() πcm.
πcm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, 、
、 分别为边
分别为边 、
、 的中点,
的中点, 是对角线,过点
是对角线,过点 作
作 交
交 的延长线于点
的延长线于点 .
.
(1)求证:
 ;
;(2)若
 ,求证:四边形
,求证:四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将这四类的人数绘制成扇形图(如图1)和条形图(如图2).
经确认扇形图是正确的,而条形图尚有一处错误.
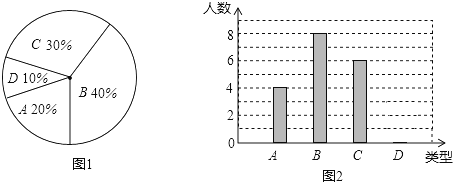
回答下列问题:
(1)写出条形图中存在的错误为________;
(2)写出这20名学生每人植树量的众数为________;中位数为________;
(3)经计算这20名学生每人植树量的平均数为5.3,则估算这260名学生共植树________棵;
(4)在这次活动中,九(1)班学生平均每人植6棵树,如果单独由男同学完成,每人应植树15棵,求如果单独由女同学完成,每人应植树多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意两个数
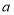 、
、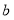 的大小比较,有下面的方法:当
的大小比较,有下面的方法:当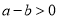 时,一定有
时,一定有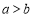 ;当
;当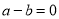 时,一定有
时,一定有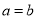 ;当
;当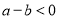 时,一定有
时,一定有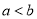 .反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:(1)已知:
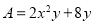 ,
,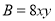 ,且
,且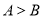 ,试判断
,试判断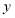 的符号;
的符号;(2)已知:
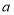 、
、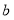 、
、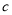 为三角形的三边,比较
为三角形的三边,比较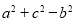 和
和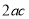 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理结论及推理说明:
如图,已知∠
 +∠
+∠ =180°,∠
=180°,∠ =∠
=∠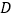 .求证:∠
.求证:∠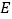 =∠
=∠ .
.证明:∵∠
 +∠
+∠ =180°(已知)
=180°(已知)∴
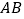 ∥
∥ ( )
( )∴∠
 = ( )
= ( )又∵∠
 =∠
=∠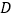 (已知)
(已知)= (等量代换)
∴
 ∥
∥ ( )
( )∴∠
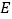 =∠
=∠ ( )
( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,平行四边形
 中,连接
中,连接 ,
, ,过点
,过点 作
作 ,垂足为
,垂足为 ,延长
,延长 与
与 相交于点
相交于点 .
.
(1)如图1,若
 ,
, ,求线段
,求线段 的长;
的长;(2)如图2,若
 ,过点
,过点 作
作 于点
于点 ,连接
,连接 、
、 .求证:
.求证: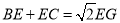 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 中,
中, ,
, 与
与 交于
交于 ,
, 为
为 延长线上的一点,且
延长线上的一点,且 ,连结
,连结 分别交
分别交 ,
, 于点
于点 ,
, ,连结
,连结 则下列结论:①
则下列结论:①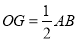 ;②与
;②与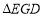 全等的三角形共有
全等的三角形共有 个;③
个;③ ;④由点
;④由点 ,
, ,
, ,
, 构成的四边形是菱形.其中正确的是( )
构成的四边形是菱形.其中正确的是( )
A.①④B.①③④C.①②③D.②③④
相关试题

