【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以2厘米/秒的速度向终点
以2厘米/秒的速度向终点![]() 移动,点
移动,点![]() 以1厘米/秒的速度向
以1厘米/秒的速度向![]() 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为
移动,当有一点到达终点时,另一点也停止运动.设运动的时间为![]() ,问:
,问:
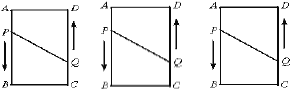
(1)当![]() 秒时,四边形
秒时,四边形![]() 面积是多少?
面积是多少?
(2)当![]() 为何值时,点
为何值时,点![]() 和点
和点![]() 距离是
距离是![]() ?
?
(3)当![]() _________时,以点
_________时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.(直接写出答案)
为顶点的三角形是等腰三角形.(直接写出答案)
参考答案:
【答案】(1)5厘米2;(2)![]() 秒或
秒或![]() 秒;(3)
秒;(3)![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
试题(1)求出BP,CQ的长,即可求得四边形BCQP面积.
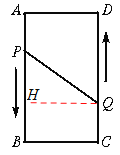
(2)过Q点作QH⊥AB于点H,应用勾股定理列方程求解即可.
(3)分PD=DQ,PD=PQ,DQ=PQ三种情况讨论即可.
(1)当t=1秒时,BP=6-2t=4,CQ=t=1,
∴四边形BCQP面积是![]() 厘米2.
厘米2.
(2)如图,过Q点作QH⊥AB于点H,则PH=BP-CQ=6-3t,HQ=2,
根据勾股定理,得![]() , 解得
, 解得![]() .
.
∴当![]() 秒或
秒或![]() 秒时,点P和点Q距离是3cm.
秒时,点P和点Q距离是3cm.
(3)∵![]() ,
,
当PD=DQ时,![]() ,解得
,解得![]() 或
或![]() (舍去);
(舍去);
当PD=PQ时,![]() ,解得
,解得![]() 或
或![]() (舍去);
(舍去);
当DQ=PQ时,![]() ,解得
,解得![]() 或
或![]() .
.
综上所述,当![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒时, 以点P、Q、D为顶点的三角形是等腰三角形.
秒时, 以点P、Q、D为顶点的三角形是等腰三角形.
-
科目: 来源: 题型:
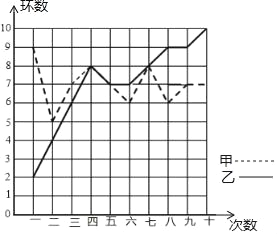
查看答案和解析>>【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=
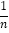 [(x1﹣
[(x1﹣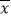 )2+(x2﹣
)2+(x2﹣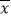 )2+…+(xn﹣
)2+…+(xn﹣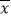 )2])
)2])平均数
方差
中位数
甲
7
7
乙
5.4
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,图2,图3是三张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,
 两点都在格点上,连结
两点都在格点上,连结 ,请完成下列作图:
,请完成下列作图: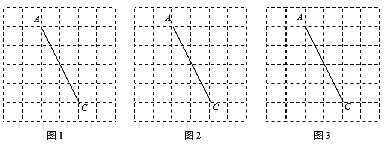
(1)以
 为对角线在图1中作一个正方形,且正方形各顶点均在格点上.
为对角线在图1中作一个正方形,且正方形各顶点均在格点上.(2)以
 为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.
为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.(3)以
 为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上.
为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.
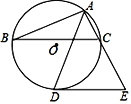
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3y2-2y+4y2;
(2)
 +4-3st-4;
+4-3st-4;(3)2(2ab+3a)-3(2a-ab);
(4)a2-[-4ab+(ab-a2)]-2ab.
(5).(-1)3-
 ÷3×[3-(-3)2];
÷3×[3-(-3)2];(6)
 ×
×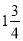 ÷(-9+19);
÷(-9+19);(7)-24×
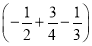 ;
;(8)(-81)÷
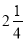 +
+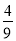 ÷(-16);
÷(-16); -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.

相关试题

