【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.
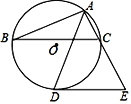
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
参考答案:
【答案】(1)DE与⊙O相切,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接DO并延长到圆上一点N,交BC于点F.由AD平分∠BAC可得![]() ,由垂径定理可得DO⊥BC,再由DE∥BC,即可推导得出;
,由垂径定理可得DO⊥BC,再由DE∥BC,即可推导得出;
(2)连接AO并延长到圆上一点M,连接BM.由DE∥BC,可推导得出∠M=60°,现利用勾股定理即可得出AB的长.
试题解析:(1)DE与⊙O相切,理由如下:
连接DO并延长到圆上一点N,交BC于点F.
∵AD平分∠BAC交⊙O于点D,∴∠BAD=∠DAC,
∴![]() ,∴DO⊥BC.
,∴DO⊥BC.
∵DE∥BC,∴∠EDO=90°,∴DE与⊙O相切;
(2)连接AO并延长到圆上一点M,连接BM.
∵DE∥BC,∴∠ACB=∠E=60°,∴∠M=60°.
∵⊙O的半径为5,∴AM=10,∴BM=5,则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,图2,图3是三张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,
 两点都在格点上,连结
两点都在格点上,连结 ,请完成下列作图:
,请完成下列作图: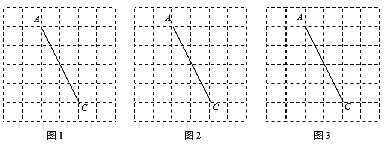
(1)以
 为对角线在图1中作一个正方形,且正方形各顶点均在格点上.
为对角线在图1中作一个正方形,且正方形各顶点均在格点上.(2)以
 为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.
为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.(3)以
 为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上.
为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中,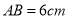 ,
, ,动点
,动点 、
、 分别从点
分别从点 、
、 同时出发,点
同时出发,点 以2厘米/秒的速度向终点
以2厘米/秒的速度向终点 移动,点
移动,点 以1厘米/秒的速度向
以1厘米/秒的速度向 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为
移动,当有一点到达终点时,另一点也停止运动.设运动的时间为 ,问:
,问: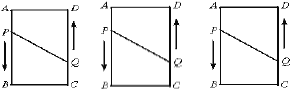
(1)当
 秒时,四边形
秒时,四边形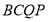 面积是多少?
面积是多少?(2)当
 为何值时,点
为何值时,点 和点
和点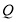 距离是
距离是 ?
?(3)当
 _________时,以点
_________时,以点 、
、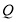 、
、 为顶点的三角形是等腰三角形.(直接写出答案)
为顶点的三角形是等腰三角形.(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3y2-2y+4y2;
(2)
 +4-3st-4;
+4-3st-4;(3)2(2ab+3a)-3(2a-ab);
(4)a2-[-4ab+(ab-a2)]-2ab.
(5).(-1)3-
 ÷3×[3-(-3)2];
÷3×[3-(-3)2];(6)
 ×
×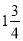 ÷(-9+19);
÷(-9+19);(7)-24×
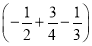 ;
;(8)(-81)÷
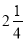 +
+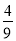 ÷(-16);
÷(-16); -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依此为2,4,6,8,...,顶点依此用A1,A2,A3,A4......表示,则顶点A55的坐标是___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=
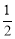 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.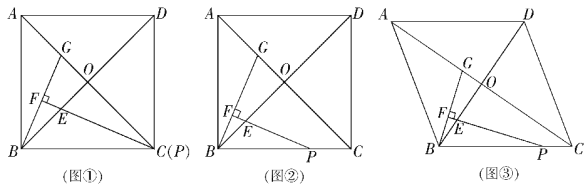
(1) 当点P与点C重合时(如图①).求证:△BOG≌△POE;(4分)
(2)通过观察、测量、猜想:
 = ,并结合图②证明你的猜想;(5分)
= ,并结合图②证明你的猜想;(5分)(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求
 的值.(用含α的式子表示)(5分)
的值.(用含α的式子表示)(5分)
相关试题

