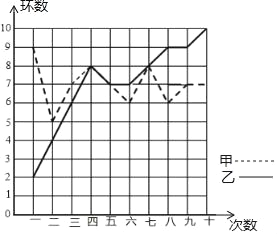
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
参考答案:
【答案】(1)1.2,7,7.5;(2)甲,乙,乙,理由见解析.
【解析】分析: (1)根据统计表,结合平均数、方差、中位数的定义,即可求出需要填写的内容.
(2)①可分别从平均数和方差两方面着手进行比较;
②可分别从平均数和中位数两方面着手进行比较;
③可从具有培养价值方面说明理由.
详解:
解:(1)甲的方差![]() [(9﹣7)2+(5﹣7)2+4×(7﹣7)2+2×(8﹣7)2+2×(6﹣7)2]=1.2,
[(9﹣7)2+(5﹣7)2+4×(7﹣7)2+2×(8﹣7)2+2×(6﹣7)2]=1.2,
乙的平均数:(2+4+6+8+7+7+8+9+9+10)÷10=7,
乙的中位数:(7+8)÷2=7.5,
填表如下:
平均数 | 方差 | 中位数 | |
甲 | 7 | 1.2 | 7 |
乙 | 7 | 5.4 | 7.5 |
(2)①从平均数和方差相结合看,甲的成绩好些;
②从平均数和中位数相结合看,乙的成绩好些;
③选乙参加.
理由:综合看,甲发挥更稳定,但射击精准度差;乙发挥虽然不稳定,但击中高靶环次数更多,成绩逐步上升,提高潜力大,更具有培养价值,应选乙.
故答案为:(1)1.2,7,7.5;(2)①甲;②乙.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
-
科目: 来源: 题型:
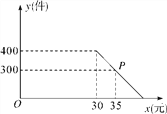
查看答案和解析>>【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b互为相反数,m,n互为倒数,x的绝对值等于3,回答:
(1)由题目可得,a+b=_______ ,mn=_______ ,x=_______ ;
(2)求多项式2x2﹣(a+b+mn)x+(a+b)2017+(﹣mn)2017的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1,图2,图3是三张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,
 两点都在格点上,连结
两点都在格点上,连结 ,请完成下列作图:
,请完成下列作图: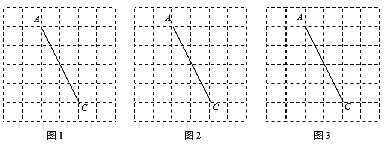
(1)以
 为对角线在图1中作一个正方形,且正方形各顶点均在格点上.
为对角线在图1中作一个正方形,且正方形各顶点均在格点上.(2)以
 为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.
为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.(3)以
 为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上.
为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中,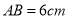 ,
, ,动点
,动点 、
、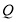 分别从点
分别从点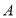 、
、 同时出发,点
同时出发,点 以2厘米/秒的速度向终点
以2厘米/秒的速度向终点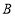 移动,点
移动,点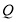 以1厘米/秒的速度向
以1厘米/秒的速度向 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为
移动,当有一点到达终点时,另一点也停止运动.设运动的时间为 ,问:
,问: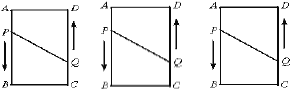
(1)当
 秒时,四边形
秒时,四边形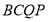 面积是多少?
面积是多少?(2)当
 为何值时,点
为何值时,点 和点
和点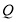 距离是
距离是 ?
?(3)当
 _________时,以点
_________时,以点 、
、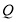 、
、 为顶点的三角形是等腰三角形.(直接写出答案)
为顶点的三角形是等腰三角形.(直接写出答案)
相关试题

