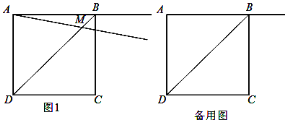
【题目】正方形ABCD的边长为2,过点A作射线AM与线段BD交于点M,∠BAM=α(0°<α<90°),作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.
(1)如图①,当0°<α<45°时,
①依题意在图①中补全图并证明:AM=CN ②当BD∥CN,求DM的值
(2)探究∠NCE与∠BAM之间的数量关系并加以证明.
参考答案:
【答案】(1)①补图见解析,证明见解析;②![]() ;(2)①当0°<α<45°时,∠NCE=2∠BAM;②当45°<α<90°时,
;(2)①当0°<α<45°时,∠NCE=2∠BAM;②当45°<α<90°时,![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.
【解析】(1)①补全的图形即可.先证明△ABM≌△CBM得AM=MC,再根据点N与点M关于直线CE对称得CM=CN,即可得到结论;
②由平行线的性质得到∠AMD=∠ANC,又由等腰三角形的性质得到∠CMN=∠CNM,由①中△ABM≌△CBM得∠AMB=∠CMB,从而∠AMD=∠CMD,进一步得到∠CMN=∠AMD=∠CMD=60°,∠ADB=45°,过点A作AG⊥BD,根据边长为2,可以求出DM的长.
(2)分两种情况讨论:①当0°<α<45°时,∠NCE=2∠BAM.作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.由△ABM≌△CBM,可得∠BAM=∠BCM,由∠ABC=∠CEA=90°,BC,AE交于一点,可得∠BAM=∠BCE,即可得到∠MCE=2∠BAM,由点N与点M关于直线CE对称,可得CN=CM,即可得到∠NCE=∠MCE,进而得出∠NCE=2∠BAM.
②当45°<α<90°时,![]() .连接CM,判定△ADM≌△CDM,即可得到∠DAM=∠DCM,再根据∠DAQ=∠ECQ,即可得到∠NCE=∠MCE=2∠DAQ,即
.连接CM,判定△ADM≌△CDM,即可得到∠DAM=∠DCM,再根据∠DAQ=∠ECQ,即可得到∠NCE=∠MCE=2∠DAQ,即![]() ,再根据∠BAM=∠BCM,∠BCM+∠DCM=90°,即可得到
,再根据∠BAM=∠BCM,∠BCM+∠DCM=90°,即可得到![]() .
.
(1)①补全的图形如图所示.
∵ABCD是正方形,∴AB=BC,∠ABM=∠CBM,BM=BM,∴△ABM≌△CBM,∴AM=MC.
∵点N与点M关于直线CE对称,∴CM=CN,∴AM=CN;
②∵BD∥CN,∴∠AMD=∠ANC.
又∵CM=CN,∴∠CMN=∠CNM,由①中△ABM≌△CBM得∠AMB=∠CMB,∴∠AMD=∠CMD,∴∠CMN=∠AMD=∠CMD=60°,∠ADB=45°.
过点A作AG⊥BD.
∵AD=2,∠ADG=45°,∴AG=DG=![]() .
.
∵∠AMD=60°,∴∠MAG=30°,∴MG=![]() ,∴DM=
,∴DM=![]() .
.
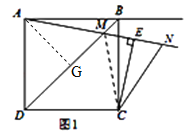
(2)①当0°<α<45°时,NCE=2∠BAM.
如图1,连接MC,∵△ABM≌△CBM,∴∠BAM=∠BCM,∵∠ABC=∠CEA=90°,BC,AE交于一点,∴∠BAM=∠BCE,∴∠MCE=2∠BAM,由点N与点M关于直线CE对称,可得CN=CM,∴∠NCE=∠MCE,∴∠NCE=2∠BAM.
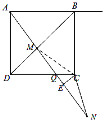
②当45°<α<90°时,![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.
如图,连接CM,∵AD=CD,∠ADM=∠CDM,DM=DM,∴△ADM≌△CDM,∴∠DAM=∠DCM.
∵∠ADQ=∠CEQ=90°,∠AQD=∠CQE,∴∠DAQ=∠ECQ,∴∠NCE=∠MCE=2∠DAQ,∴∠DCM=![]() ∠NCE.
∠NCE.
∵∠BAM=∠BCM,∠BCM+∠DCM=90°,∴![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=
 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>

 的x的取值范围;
的x的取值范围;(3)若点P在x轴上,且S△ACP=
 S△BOC,求点P的坐标.
S△BOC,求点P的坐标.
-
科目: 来源: 题型:
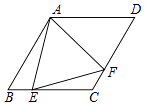
查看答案和解析>>【题目】如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】结算下列各题
(1)计算:|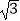 ﹣2|+(
﹣2|+(  )﹣1﹣(π﹣3.14)0﹣
)﹣1﹣(π﹣3.14)0﹣ 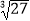 ;
;
(2)计算:[xy(3x﹣2)﹣y(x2﹣2x)]÷x2y. -
科目: 来源: 题型:
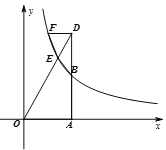
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(a,0)(其中a>0),作AB∥y轴交反比例函数
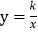 (k>0,x>0)的图象于点B.
(k>0,x>0)的图象于点B.(1)当△OAB的面积为2时,①求k的值;②若a=2,过A点作AC∥OB交
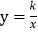 (k>0,x>0)图象于点C,求C的横坐标;
(k>0,x>0)图象于点C,求C的横坐标;(2)若D为射线AB上一点,连接OD交反比例函数图象于点E,DF∥x轴交反比例函数
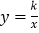 (k>0,x>0)的图象于点F,连接EF、EB,试猜想:
(k>0,x>0)的图象于点F,连接EF、EB,试猜想: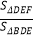 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出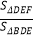 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.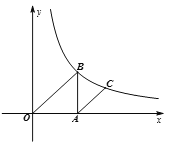
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是;
(2)据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、92、85.
①这组数据的众数是 , 中位数是;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人 ? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程
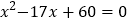 的两个根,则△ABC的周长为 ______.
的两个根,则△ABC的周长为 ______.
相关试题

