【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

参考答案:
【答案】(1)y=![]() x+2;(2)﹣6<x<0或x>2;(3)(﹣2,0)或(﹣6,0)
x+2;(2)﹣6<x<0或x>2;(3)(﹣2,0)或(﹣6,0)
【解析】分析:(1)把点A、B的坐标分别代入反比例函数解析式中,求出m、n的值,得到点A、B的坐标,再将点A、B的坐标分别代入一次函数解析式中即可确定出一次函数解析式;
(2)结合图象,根据两函数的交点横坐标,找出一次函数图象在反比例图象上方时x的范围即可;
(3)先求出△BOC的面积,再根据S△ACP=![]() S△BOC求出CP的长,进而得到点P的坐标.
S△BOC求出CP的长,进而得到点P的坐标.
详解:(1)将A(m,3)代入反比例解析式得:m=2,则A(2,3),
将B(-6,n)代入反比例解析式得:n=-1,则B(-6,-1),
将A与B的坐标代入y=kx+b得:![]() ,
,
解得:![]() ,
,
则一次函数解析式为y=![]() x+2;
x+2;
(2)由图象得:![]() x+2>
x+2>![]() 的x的取值范围是:-6<x<0或x>2;
的x的取值范围是:-6<x<0或x>2;
(3)∵y=![]() x+2中,y=0时,
x+2中,y=0时,![]() x+2=0,
x+2=0,
解得x=-4,则C(-4,0),OC=4
∴△BOC的面积=![]() ×4×1=2,
×4×1=2,
∴S△ACP=![]() S△BOC=
S△BOC=![]() ×2=3.
×2=3.
∵S△ACP=![]() CP×3=
CP×3=![]() CP,
CP,
∴![]() CP=3,
CP=3,
∴CP=2,
∵C(-4,0),
∴点P的坐标为(-2,0)或(-6,0).
-
科目: 来源: 题型:
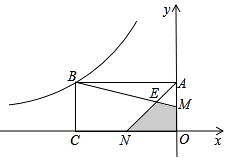
查看答案和解析>>【题目】如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
A.y=﹣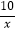
B.y=﹣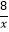
C.y=﹣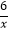
D.y=﹣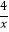
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的底边长为10cm,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长5cm,那么这个三角形的腰长为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A. 20千米/小时 B. 60千米/小时
C. 25千米/小时 D. 75千米小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于 .
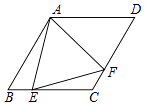
-
科目: 来源: 题型:
查看答案和解析>>【题目】结算下列各题
(1)计算:|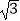 ﹣2|+(
﹣2|+(  )﹣1﹣(π﹣3.14)0﹣
)﹣1﹣(π﹣3.14)0﹣ 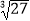 ;
;
(2)计算:[xy(3x﹣2)﹣y(x2﹣2x)]÷x2y. -
科目: 来源: 题型:
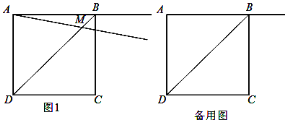
查看答案和解析>>【题目】正方形ABCD的边长为2,过点A作射线AM与线段BD交于点M,∠BAM=α(0°<α<90°),作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.
(1)如图①,当0°<α<45°时,
①依题意在图①中补全图并证明:AM=CN ②当BD∥CN,求DM的值
(2)探究∠NCE与∠BAM之间的数量关系并加以证明.
相关试题

