【题目】某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是;
(2)据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、92、85.
①这组数据的众数是 , 中位数是;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人 ?
参考答案:
【答案】
(1)![]()
(2)90;89.5;200人
【解析】解:(1.)列表如下:1表示“立定跳远”,2表示“耐久跑”,3表示“掷实心球”,4表示“引体向上”
1 | 2 | 3 | 4 | |
1 | ﹣﹣﹣ | (2,1) | (3,1) | (4,1) |
2 | (1,2) | ﹣﹣﹣ | (3,2) | (4,2) |
3 | (1,3) | (2,3) | ﹣﹣﹣ | (4,3) |
4 | (1,4) | (2,4) | (3,4) | ﹣﹣﹣ |
所有等可能的情况数为12种,其中恰好抽到“立定跳远”,“耐久跑”两项的情况有2种,则P= ![]() =
= ![]() ,
,
故答案为: ![]() ;
;
(2.)①根据数据得:众数为90;中位数为89.5,
故答案为:90;89.5;
(1)列表得出所有等可能的情况数,找出恰好抽到“立定跳远”,“耐久跑”两项的情况数,即可求出所求的概率;(2)①根据已知数据确定出众数与中位数即可;②求出成绩不低于90分占的百分比,乘以400即可得到结果.
②解:12名男生中达到优秀的共有6人,根据题意得: ![]() ×400=200(人),
×400=200(人),
则估计初三年级400名男生中“立定跳远”成绩为优秀的学生约为200人
-
科目: 来源: 题型:
查看答案和解析>>【题目】结算下列各题
(1)计算:|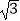 ﹣2|+(
﹣2|+(  )﹣1﹣(π﹣3.14)0﹣
)﹣1﹣(π﹣3.14)0﹣ 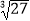 ;
;
(2)计算:[xy(3x﹣2)﹣y(x2﹣2x)]÷x2y. -
科目: 来源: 题型:
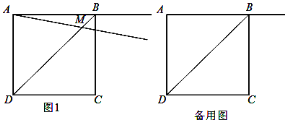
查看答案和解析>>【题目】正方形ABCD的边长为2,过点A作射线AM与线段BD交于点M,∠BAM=α(0°<α<90°),作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.
(1)如图①,当0°<α<45°时,
①依题意在图①中补全图并证明:AM=CN ②当BD∥CN,求DM的值
(2)探究∠NCE与∠BAM之间的数量关系并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(a,0)(其中a>0),作AB∥y轴交反比例函数
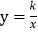 (k>0,x>0)的图象于点B.
(k>0,x>0)的图象于点B.(1)当△OAB的面积为2时,①求k的值;②若a=2,过A点作AC∥OB交
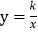 (k>0,x>0)图象于点C,求C的横坐标;
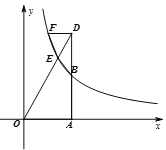
(k>0,x>0)图象于点C,求C的横坐标;(2)若D为射线AB上一点,连接OD交反比例函数图象于点E,DF∥x轴交反比例函数
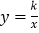 (k>0,x>0)的图象于点F,连接EF、EB,试猜想:
(k>0,x>0)的图象于点F,连接EF、EB,试猜想: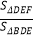 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出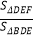 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.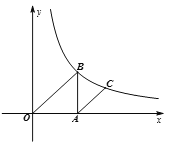
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程
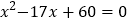 的两个根,则△ABC的周长为 ______.
的两个根,则△ABC的周长为 ______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC. ①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.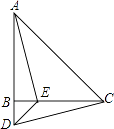
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=kx+b与双曲线y2=
 交于A、B两点,它们的横坐标分别为1和5.
交于A、B两点,它们的横坐标分别为1和5. 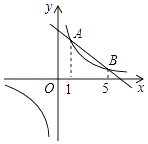
(1)当m=5时,求直线AB的解析式及△AOB的面积;
(2)当y1>y2时,直接写出x的取值范围.
相关试题

