搜索
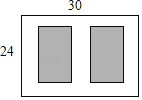
【题目】如图，某小区有一块长为30 m，宽为24 m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为480 m2，两块绿地之间及周边有宽度相等的人行通道，则人行通道的宽度为________m．
参考答案：
【答案】2
【解析】
试题设人行通道的宽度为x米，将两块矩形绿地合在一起长为（30﹣3x）m，宽为（24﹣2x）m，根据矩形绿地的面积为480m2，即可列出关于x的一元二次方程，解方程即可得出x的值，经检验后得出x=20不符合题意，此题得解．
试题解析：设人行通道的宽度为x米，将两块矩形绿地合在一起长为（30﹣3x）m，宽为（24﹣2x）m，
由已知得：（30﹣3x）（24﹣2x）=480，
整理得：x2﹣22x+40=0，
解得：x1=2，x2=20，
当x=20时，30﹣3x=﹣30，24﹣2x=﹣16，
不符合题意，
故人行通道的宽度为2米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，M、N分别是边AD、BC的中点，点P、Q在DC边上，且PQ=
DC．若AB=16，BC=20，则图中阴影部分的面积是 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】说理填空：如图，点E是DC的中点，EC=EB，∠CDA=120°，DF//BE，且DF平分∠CDA，求证：△BEC为等边三角形．
解： 因为DF平分∠CDA（已知）
所以∠FDC=
∠________． （ ）因为∠CDA=120°（已知）
所以∠FDC=______°．
因为DF//BE（已知）
所以∠FDC=∠_________．（____________________________________）
所以∠BEC = 60°，又因为EC=EB，（已知）
所以△BCE为等边三角形．（_____________________________）
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算题
（1）解方程：（x+1）2=9；
（2）解方程：x2﹣4x+2=0． -
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形，那么我们称这个三角形为“活三角形”，这条直线称为该“活三角形”的“生命线”．
（1）小明在研究“活三角形”问题时（如图），他发现，在△ABC中，若∠BAC = 3∠C时，这个△ABC一定是“活三角形”．点D在BC边上一点，联结AD，他猜测：当∠DAC = ∠C时，AD就是这个三角形的“生命线”，请你帮他说明AD是△ABC的“生命线”的理由．
（2）如小明研究结果可以总结为：有一个内角是另一个内角的3倍时，该三角形是一个“活三角形”．
请通过自己操作研究，并根据上诉结论，总结“活三角形”的其他特征．
（注意从三角形边、角特征及相互间关系总结）
，该三角形是一个“活三角形”．
，该三角形是一个“活三角形”．
（3）如果一个等腰三角形是一个“活三角形”那么它的顶角大小为： 度．（直接写出结果即可）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1=∠2，∠5=∠6，∠3=∠4，试说明AE∥BD，AD∥BC．请完成下列证明过程．
证明：
∵∠5=∠6，
∴AB∥CE( )，
∴∠3=__________
∵∠3=∠4，
∴∠4=∠BDC( )，
∴ ∥BD( )，
∴∠2= ( )
∵∠1=∠2，
∴∠1=______，
∴AD∥BC
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠1＋∠2=180°，∠A=∠C，DA平分∠BDF．
（1）求证：AE∥CF．
（2）BC平分∠DBE吗？为什么？
相关试题
