搜索
【题目】计算题
（1）解方程：（x+1）2=9；
（2）解方程：x2﹣4x+2=0．
参考答案：
【答案】
（1）解：两边开方得：x+1=±3，
解得：x1=2，x2=﹣4；
（2）解：这里a=1，b=﹣4，c=2，
b2﹣4ac=8＞0，
x= 
=2± 
，
即x1=2+ ，x2=2﹣ ．
【解析】根据直接开平方法求出x的值；利用公式法求出方程的解.
【考点精析】本题主要考查了直接开平方法和公式法的相关知识点，需要掌握方程没有一次项，直接开方最理想．如果缺少常数项，因式分解没商量．b、c相等都为零，等根是零不要忘．b、c同时不为零，因式分解或配方，也可直接套公式，因题而异择良方；要用公式解方程，首先化成一般式．调整系数随其后，使其成为最简比．确定参数abc，计算方程判别式．判别式值与零比，有无实根便得知．有实根可套公式，没有实根要告之才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC＝13厘米，BC＝10厘米，AD⊥BC于点D，动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动，设动点运动时间为t秒.
(1)求AD的长；
(2)当P、C两点的距离为
时，求t的值；(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t值，使得
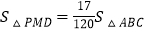？若存在，请求出t的值；若不存在，请说明理由．
备用图
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，M、N分别是边AD、BC的中点，点P、Q在DC边上，且PQ=
DC．若AB=16，BC=20，则图中阴影部分的面积是 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】说理填空：如图，点E是DC的中点，EC=EB，∠CDA=120°，DF//BE，且DF平分∠CDA，求证：△BEC为等边三角形．
解： 因为DF平分∠CDA（已知）
所以∠FDC=
∠________． （ ）因为∠CDA=120°（已知）
所以∠FDC=______°．
因为DF//BE（已知）
所以∠FDC=∠_________．（____________________________________）
所以∠BEC = 60°，又因为EC=EB，（已知）
所以△BCE为等边三角形．（_____________________________）
-
科目： 来源： 题型：
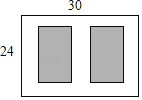
查看答案和解析>>【题目】如图，某小区有一块长为30 m，宽为24 m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为480 m2，两块绿地之间及周边有宽度相等的人行通道，则人行通道的宽度为________m．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形，那么我们称这个三角形为“活三角形”，这条直线称为该“活三角形”的“生命线”．
（1）小明在研究“活三角形”问题时（如图），他发现，在△ABC中，若∠BAC = 3∠C时，这个△ABC一定是“活三角形”．点D在BC边上一点，联结AD，他猜测：当∠DAC = ∠C时，AD就是这个三角形的“生命线”，请你帮他说明AD是△ABC的“生命线”的理由．
（2）如小明研究结果可以总结为：有一个内角是另一个内角的3倍时，该三角形是一个“活三角形”．
请通过自己操作研究，并根据上诉结论，总结“活三角形”的其他特征．
（注意从三角形边、角特征及相互间关系总结）
，该三角形是一个“活三角形”．
，该三角形是一个“活三角形”．
（3）如果一个等腰三角形是一个“活三角形”那么它的顶角大小为： 度．（直接写出结果即可）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1=∠2，∠5=∠6，∠3=∠4，试说明AE∥BD，AD∥BC．请完成下列证明过程．
证明：
∵∠5=∠6，
∴AB∥CE( )，
∴∠3=__________
∵∠3=∠4，
∴∠4=∠BDC( )，
∴ ∥BD( )，
∴∠2= ( )
∵∠1=∠2，
∴∠1=______，
∴AD∥BC
相关试题
