搜索
【题目】如图，∠1＋∠2=180°，∠A=∠C，DA平分∠BDF．
（1）求证：AE∥CF．
（2）BC平分∠DBE吗？为什么？
参考答案：
【答案】（1）见详解；（2）BC平分∠DBE，证明见详解．
【解析】
（1）根据同角的补角相等，证明∠2=∠DBE，问题得证；
（2）先证明AD∥BC，进而证明∠C=∠CBD，再根据AE∥CF，证明∠CBD=∠CBE，问题得证．
解：（1）证明：∵∠1＋∠2=180°，∠1＋∠DBE=180°，
∴∠2=∠DBE，
∴AE∥CF；
（2）BC平分∠DBE，
证明：∵AE∥CF，
∴∠C+∠CBA=180°，
∵∠A=∠C，
∴∠A+∠CBA=180°，
∴AD∥BC，
∴∠ADB=∠CBD，∠FDA=∠C，
∵DA平分∠BDF，
∴∠FDA=∠ADB，
∴∠C=∠CBD，
∵AE∥CF，
∴∠C=∠CBE，
∴∠CBD=∠CBE，
∴BC平分∠DBE．
-
科目： 来源： 题型：
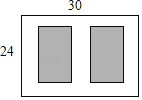
查看答案和解析>>【题目】如图，某小区有一块长为30 m，宽为24 m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为480 m2，两块绿地之间及周边有宽度相等的人行通道，则人行通道的宽度为________m．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形，那么我们称这个三角形为“活三角形”，这条直线称为该“活三角形”的“生命线”．
（1）小明在研究“活三角形”问题时（如图），他发现，在△ABC中，若∠BAC = 3∠C时，这个△ABC一定是“活三角形”．点D在BC边上一点，联结AD，他猜测：当∠DAC = ∠C时，AD就是这个三角形的“生命线”，请你帮他说明AD是△ABC的“生命线”的理由．
（2）如小明研究结果可以总结为：有一个内角是另一个内角的3倍时，该三角形是一个“活三角形”．
请通过自己操作研究，并根据上诉结论，总结“活三角形”的其他特征．
（注意从三角形边、角特征及相互间关系总结）
，该三角形是一个“活三角形”．
，该三角形是一个“活三角形”．
（3）如果一个等腰三角形是一个“活三角形”那么它的顶角大小为： 度．（直接写出结果即可）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠1=∠2，∠5=∠6，∠3=∠4，试说明AE∥BD，AD∥BC．请完成下列证明过程．
证明：
∵∠5=∠6，
∴AB∥CE( )，
∴∠3=__________
∵∠3=∠4，
∴∠4=∠BDC( )，
∴ ∥BD( )，
∴∠2= ( )
∵∠1=∠2，
∴∠1=______，
∴AD∥BC
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中正确的是（ ）.
A. “打开电视机，正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为
，说明每买1000张，一定有一张中奖C. 抛掷一枚质地均匀的硬币一次，出现正面朝上的概率为
D. 想了解长沙市所有城镇居民的人均年收入水平，宜采用抽样调查
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请在右边的平面直角坐标系中描出以下三点：
、
、
并回答如下问题：
在平面直角坐标系中画出△ABC；
在平面直角坐标系中画出△A′B′C′；使它与
关于x轴对称，并写出点C′的坐标______；
判断△ABC的形状，并说明理由．
相关试题
