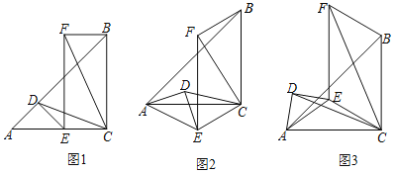
【题目】如图1,已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC为边作平行四边形CEFB,连CD、CF.
(1)如图2,△ADE绕点A旋转一定角度,求证:CD=![]() CF;
CF;
(2)如图3,AE=![]() ,AB=
,AB=![]() ,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,求CF的长.
,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,求CF的长.
参考答案:
【答案】(1)见解析 (2)6或4
【解析】
(1)连接FD,证明△ADC≌△EDF(SAS),推出△DFC为等腰直角三角形即可解决问题;
(2)分两种情形分别画出图形,利用(1)中结论求出CD即可解决问题.
(1)解:连接FD,设DE与AC交于点G
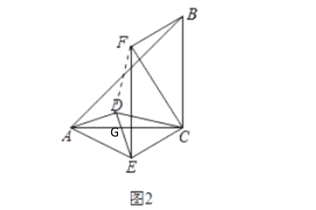
∵四边形CEFB是平行四边形
∴BC∥EF
∵AC⊥BC
∴EF⊥AC
∵AD⊥DE,EF⊥AC,∠DGA=∠CGE
∴∠DAC=∠DEF,
又∵AD=ED,AC=EF,
∴△ADC≌△EDF(SAS),
∴DC=DF,∠ADC=∠EDF,即∠ADE+∠EDC=∠FDC+∠EDC,
∴∠FDC=∠ADE=90°,
∴△DFC为等腰直角三角形,
∴CD=![]() CF;
CF;
(2)解:如图,设AE与CD的交点为M,
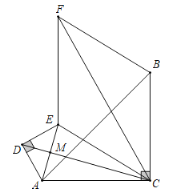
∵四边形CEFB为菱形
∴CE=CB
∵△ADE、△ACB为等腰直角三角形
∴CA=CB
∴CE=CA,
∵DE=DA,
∴CD垂直平分AE,
∵AE=![]() ,AB=
,AB=![]()
∴DM=EM=![]() AE=
AE=![]() ,AC=BC=
,AC=BC=![]() AB=
AB=![]()
∴CE=![]()
∴CM=![]() =
=![]() ,
,
∴CD=DM+CM=![]() ,
,
∵CF=![]() CD,
CD,
∴CF=6;
如图,设AE与CD的交点为M,
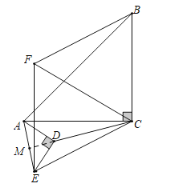
同法可得CD=CM-DM=![]() -
-![]() =
=![]() ,
,
∴CF=![]() CD=4;
CD=4;
综上所述,满足条件的CF的值为6或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】动点P在□ABCD边上沿着
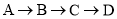 的方向匀速移动,到达点
的方向匀速移动,到达点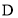 时停止移动.已知P的速度为
时停止移动.已知P的速度为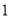 个单位长度/
个单位长度/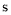 ,其所在位置用点
,其所在位置用点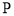 表示,
表示,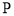 到对角线
到对角线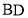 的距离(即垂线段
的距离(即垂线段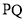 的长)为
的长)为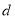 个单位长度,其中
个单位长度,其中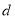 与
与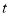 的函数图像如图②所示.
的函数图像如图②所示.(1)若a=3,求当t=8时△BPQ的面积;
(2)如图②,点M,N分别在函数第一和第三段图像上,线段
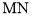 平行于横轴,
平行于横轴,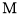 、
、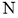 的横坐标分别为
的横坐标分别为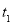 、
、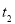 .设
.设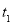 、
、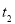 时点P走过的路程分别为
时点P走过的路程分别为 、
、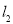 ,若
,若 +
+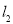 =16,求
=16,求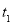 、
、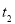 的值.
的值.
-
科目: 来源: 题型:
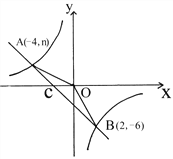
查看答案和解析>>【题目】如图,已知A(-4,n)、B(2,-6)是一次函数y1=k1x+b与反比例函数y2=
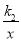 的两个交点,直线AB与x轴交于点C。
的两个交点,直线AB与x轴交于点C。(1)求两函数解析式;(2)求△AOB的面积;
(3)根据图象回答:y1<y2时,自变量x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,直线y=x+m和抛物线y=
 +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),B(3,2).

(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角板的直角顶点
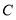 按如图方式叠放在一起,友情提示:
按如图方式叠放在一起,友情提示: ,
,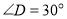 ,
,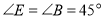 .
.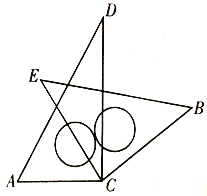
(1)①若
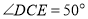 ,则
,则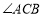 的度数为__________;
的度数为__________;②若
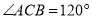 ,则
,则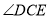 的度数为__________.
的度数为__________.(2)由(1)猜想
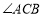 与
与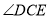 的数量关系,并说明理由;
的数量关系,并说明理由;(3)当
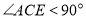 且点
且点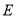 在直线
在直线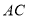 的上方时,当这两块角尺有一组边互相平行时,请直接写出
的上方时,当这两块角尺有一组边互相平行时,请直接写出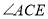 角度所有可能的值.
角度所有可能的值. -
科目: 来源: 题型:
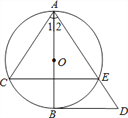
查看答案和解析>>【题目】如图,AB为⊙O的直径,劣弧BC=劣弧BE,BD∥CE,连接AE并延长交BD于D.
求证:(1)AC=AE;
(2)AB2=ACAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,试问
,试问 与
与 平行吗?为什么?
平行吗?为什么?下面是说明
 的过程,请在( )内写上理由.
的过程,请在( )内写上理由.
解:
 ,
, ( )
( ) ( )
( )又
 ,
, (等量代换)
(等量代换) ( )
( )
相关试题

