【题目】动点P在□ABCD边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知P的速度为
时停止移动.已知P的速度为![]() 个单位长度/
个单位长度/![]() ,其所在位置用点
,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
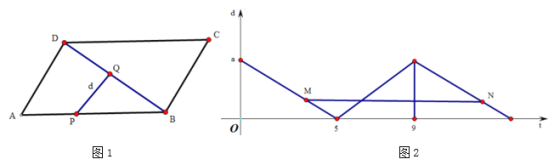
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)若a=3,求当t=8时△BPQ的面积;
(2)如图②,点M,N分别在函数第一和第三段图像上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() .设
.设![]() 、
、![]() 时点P走过的路程分别为
时点P走过的路程分别为![]() 、
、![]() ,若
,若![]() +
+![]() =16,求
=16,求![]() 、
、![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)3.5;12.5
;(2)3.5;12.5
【解析】
(1)由题意知:当a=3时,点P在A点,此时PQ最长为a,即此时PQ=3,当P点运动到点B时,此点P和点B重合,即PQ为0,则此时P点运动路程为AB的长度,由图象可知AB=5,当点P继续运动到点C时,此时PQ最长即PQ=3,可推出AB=CD=5,AD=BC=4,可得当t=8时,P点在BC边上,即AB+BP=8,则BP=3,即对应的时间是t=5和t=9之间的函数图象,求出这一段的函数解析式,再把t=8代入,求出对应的d,即可求出BQ,则可求出△BPQ的面积;
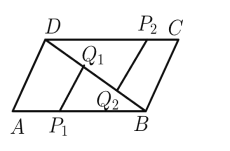
(2)由题意可得l1=t1,l2=t2,即t1+t2=16①,再根据M,N平行于x轴,可推出AP1=CP2,即t1=t2-9②,联立①,②即可求出![]() 、
、![]() 的值.
的值.
(1)如图:

由题意知:当a=3时,点P在A点,此时PQ最长为a,即此时PQ=3,
当P点运动到点B时,此点P和点B重合,即PQ为0,
则此时P点运动路程为AB的长度,由图象可知AB=5,
当点P继续运动到点C时,此时PQ最长即PQ=3,(用全等三角形可易证,
此BC的长度为:BC=9-5=4,
即AB=CD=5,AD=BC=4,
∴当t=8时,P点在BC边上,即AB+BP=8,则BP=3,
则对应的时间是t=5和t=9之间的函数图象,
设此时函数为d=kt+b,把(5,0),(9,3)代入函数则有![]() ,
,
解得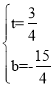 ,
,
∴d=![]() t
t![]() ,
,
把t=8代入,则d=![]() ×8
×8![]() =
=![]() ,
,
在△BPQ中,BQ=![]() =
=![]() ,
,
∴S△BPQ=![]() BQ·PQ=
BQ·PQ=![]() ×
×![]() ×
×![]() =
=![]() ;
;
(2)由题意可得l1=t1,l2=t2,
∵l1+l2=16,
∴t1+t2=16①,
∵MN平行于x轴,
∴yM=yN,
即此时d的值相同,
∴AP1=CP2,
即t1=t2-9②,
联立①,②得: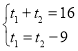 ,
,
解得: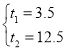 ,
,
∴t1=3.5,t2=12.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂从2011年起开始投入技改资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表所示:
年度
2011
2012
2013
2014
投入技改资金
 /万元
/万元2.5
3
4
4.5
产品成本
 /(万元/件)
/(万元/件)7.2
6
4.5
4
(1)请认真分析表中的数据,从你学过的一次函数和反比例函数中确定哪种函数能表示其变化规律,并求出它的表达式;
(2)按照这种变化规律,2015年已投入技改资金5万元.
①预计产品成本每件比2014年降低多少万元?
②如果打算在2015年把每件产品的成本降低到3.2万元,那么还需投入技改资金多少万元?(精确到0.01万元)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为66万元;本周已售出2辆A型车和1辆B型车,销售额为42万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过84万元.问最多可以购买多少辆B型号的新能源汽车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的南偏东60方向,距离灯塔100海里的A处,它计划去往位于灯塔P的北偏东45方向上的B处.(参考数据
 ≈1.414,
≈1.414,  ≈1.732,
≈1.732,  ≈2.449)
≈2.449)(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔190海里的点O处.圆形暗礁区域的半径为50海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险,并说明理由.

-
科目: 来源: 题型:
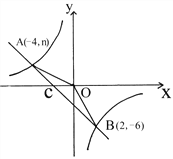
查看答案和解析>>【题目】如图,已知A(-4,n)、B(2,-6)是一次函数y1=k1x+b与反比例函数y2=
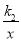 的两个交点,直线AB与x轴交于点C。
的两个交点,直线AB与x轴交于点C。(1)求两函数解析式;(2)求△AOB的面积;
(3)根据图象回答:y1<y2时,自变量x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,直线y=x+m和抛物线y=
 +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),B(3,2).

(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC为边作平行四边形CEFB,连CD、CF.
(1)如图2,△ADE绕点A旋转一定角度,求证:CD=
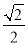 CF;
CF;(2)如图3,AE=
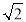 ,AB=
,AB=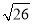 ,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,求CF的长.
,将△ADE绕A点旋转一周,当四边形CEFB为菱形时,求CF的长.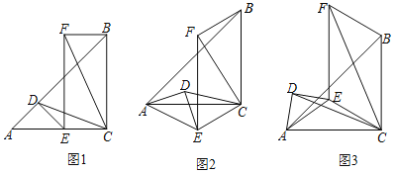
相关试题

