【题目】如图,从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC.
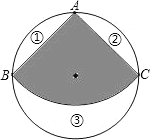
(1)求这个扇形的面积;
(2)若将扇形BAC围成一个圆锥的侧面,这个圆锥的底面直径是多少?能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
参考答案:
【答案】(1)S扇形=![]() ;(2)不能,见解析
;(2)不能,见解析
【解析】
试题分析:(1)由勾股定理求扇形的半径,再根据面积公式求值;
(2)利用底面周长等于展开图的弧长,可求得直径的长度,进而比较圆锥的底面半径和图中EF的大小关系即可.
解:(1)∵∠A为直角,
∴直径BC=2,
∴根据勾股定理得:AB2+AC2=BC2,
∵AB=AC,
∴AB2+AB2=22,
∴扇形半径为AB=![]() ;
;
∴S扇形=![]() ;
;
(2)设围成圆锥的底面半径为r,则2πr=![]() ,解得
,解得![]() ;
;
延长AO分别交弧BC和⊙O于E、F,而EF=2![]() <
<![]() ;
;
∴不能从最大的余料③中剪出一个圆做该圆锥的底面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数
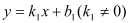 的图象为直线
的图象为直线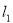 ,一次函数
,一次函数 的图象为直线
的图象为直线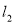 ,若
,若 ,且
,且 ,我们就称直线
,我们就称直线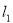 与直线
与直线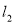 互相平行.已知一次函数
互相平行.已知一次函数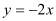 的图象为直线
的图象为直线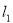 ,过点
,过点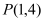 且与已知直线
且与已知直线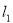 平行的直线为
平行的直线为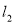 。
。解答下面的问题:
(1)求
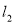 的函数表达式;
的函数表达式;(2)设直线
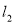 分别与
分别与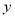 轴、
轴、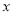 轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求
轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求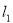 和
和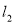 两平行线之间的距离 ;
两平行线之间的距离 ;(3)若Q为OA上一动点,求QP+QB的最小值,并求取得最小值时Q点的坐标。
(4)在
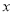 轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等边△ABC内接于⊙O,点P是劣弧
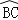 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.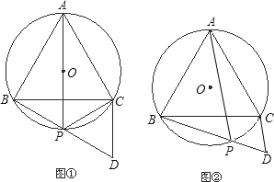
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
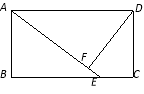
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.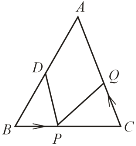
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若
 ,求出发几秒后,
,求出发几秒后, 为直角三角形?
为直角三角形?(3)若
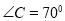 ,当
,当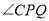 的度数为多少时,
的度数为多少时, 为等腰三角形?(请直接写出答案,不必写出过程).
为等腰三角形?(请直接写出答案,不必写出过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】今年3月5日,实验中学组织全体学生参加了“走出校门,服务社会”的活动。九年级一班小明同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图。请根据小明同学所作的两个图形,解答:
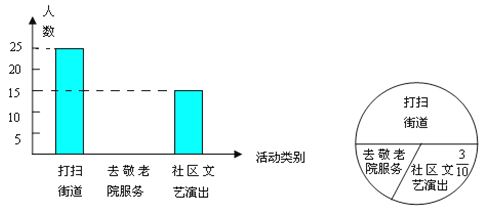
(1)九年级一班有多少名学生?
(2)补全直方图的空缺部分。
(3)若九年级有800名学生,估计该年级去敬老院的人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面有8个算式,排成4行2列
2+2, 2×2
3+
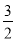 , 3×
, 3×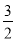
4+
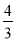 , 4×
, 4×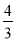
5+
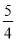 , 5×
, 5×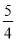
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+
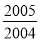 和2005×
和2005×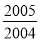 的结果相等吗?
的结果相等吗?
相关试题

