【题目】在![]() 中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
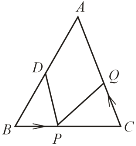
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若![]() ,求出发几秒后,
,求出发几秒后,![]() 为直角三角形?
为直角三角形?
(3)若![]() ,当
,当![]() 的度数为多少时,
的度数为多少时,![]() 为等腰三角形?(请直接写出答案,不必写出过程).
为等腰三角形?(请直接写出答案,不必写出过程).
参考答案:
【答案】(1)2.5cm/s;(2)2.5秒或10秒;(3)70°.
【解析】
试题分析:(1)根据等边对等角可得∠B=∠C,然后表示出BD、BP、PC、CQ,再根据全等三角形对应边相等,分①BD、PC是对应边,②BD与CQ是对应边两种情况讨论求解即可.(2)分类讨论①∠BDP和∠BPD两种情况讨论,然后根据直角三角形中30°角所对的直角边等于斜边的一半得出结论.
试题解析:(1)![]() ,
,![]() ,
, ![]() cm,D是AB的中点,
cm,D是AB的中点,![]() cm .
cm .![]() 点Q的速度与点P的速度不同,
点Q的速度与点P的速度不同,![]() ,要使△BPD和△CQP全等,则BP=CP=8cm,CQ=BD= 10cm ,
,要使△BPD和△CQP全等,则BP=CP=8cm,CQ=BD= 10cm , ![]() 秒 ,
秒 , ![]() cm/s .
cm/s .
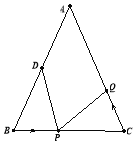
(2)【1】当![]() 时,
时, ![]() ∴
∴ ![]() ,∴ 2 BP = BD = 10
,∴ 2 BP = BD = 10
∴ BP = 5 即2 x = 5 ∴x = 2.5.
【2】当![]() 时,
时,![]() ∴
∴ ![]() ,∴ BP = 2 BD = 20, 即2 x = 20 ∴x = 10
,∴ BP = 2 BD = 20, 即2 x = 20 ∴x = 10
![]() 当P出发2.5秒或10秒后,
当P出发2.5秒或10秒后,![]() 为直角三角形
为直角三角形
(3)![]() ,
,![]() ,
,![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等边△ABC内接于⊙O,点P是劣弧
 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.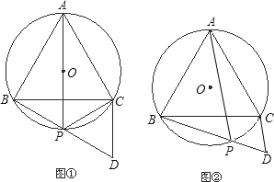
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
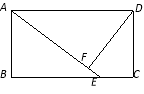
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC.
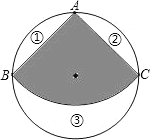
(1)求这个扇形的面积;
(2)若将扇形BAC围成一个圆锥的侧面,这个圆锥的底面直径是多少?能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年3月5日,实验中学组织全体学生参加了“走出校门,服务社会”的活动。九年级一班小明同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图。请根据小明同学所作的两个图形,解答:
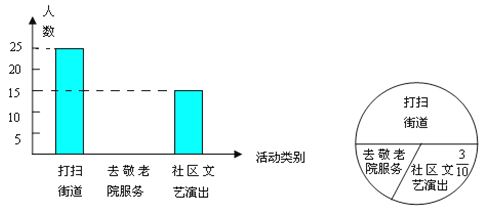
(1)九年级一班有多少名学生?
(2)补全直方图的空缺部分。
(3)若九年级有800名学生,估计该年级去敬老院的人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面有8个算式,排成4行2列
2+2, 2×2
3+
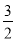 , 3×
, 3×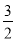
4+
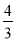 , 4×
, 4×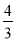
5+
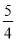 , 5×
, 5×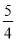
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+
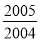 和2005×
和2005×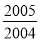 的结果相等吗?
的结果相等吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实国务院惠农的指示精神,最近市政府又出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量
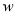 (千克)与销售价
(千克)与销售价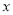 (元/千克)有如下关系:
(元/千克)有如下关系: .设这种产品每天的销售利润为
.设这种产品每天的销售利润为 (元).
(元).(1)求
 与
与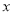 之间的函数关系式.
之间的函数关系式.(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
相关试题

