【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数![]() 的图象为直线
的图象为直线![]() ,一次函数
,一次函数![]() 的图象为直线
的图象为直线![]() ,若
,若![]() ,且
,且![]() ,我们就称直线
,我们就称直线![]() 与直线
与直线![]() 互相平行.已知一次函数
互相平行.已知一次函数![]() 的图象为直线
的图象为直线![]() ,过点
,过点![]() 且与已知直线
且与已知直线![]() 平行的直线为
平行的直线为![]() 。
。
解答下面的问题:
(1)求![]() 的函数表达式;
的函数表达式;
(2)设直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求
轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求![]() 和
和![]() 两平行线之间的距离 ;
两平行线之间的距离 ;
(3)若Q为OA上一动点,求QP+QB的最小值,并求取得最小值时Q点的坐标。
(4)在![]() 轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() , Q(0,3)(4)M(-1,0)或M(-2,0)或
, Q(0,3)(4)M(-1,0)或M(-2,0)或![]() 或
或![]() .
.
【解析】
试题分析:(1)设直线![]() 的解析式为
的解析式为![]() ,把点
,把点![]() 代入求出b的值即可;(2)利用直线
代入求出b的值即可;(2)利用直线![]() 求出点A、B的坐标得出OA,OB的长,利用勾股定理得到AB的长,然后利用三角形的面积求出OC的长即可;(3)求出点B关于y轴的对称点B′(-3,0),连结B′P交y轴于Q,即可求解;(4)求出BP的长,分BP=BM,BP=PM,MB=MP三种情况讨论.
求出点A、B的坐标得出OA,OB的长,利用勾股定理得到AB的长,然后利用三角形的面积求出OC的长即可;(3)求出点B关于y轴的对称点B′(-3,0),连结B′P交y轴于Q,即可求解;(4)求出BP的长,分BP=BM,BP=PM,MB=MP三种情况讨论.
试题解析:
(1)∵![]() ∥
∥![]() , ∴ 设直线
, ∴ 设直线![]() 的解析式
的解析式
为![]() ,
,
把点![]() 代入得,
代入得,![]()
∴ ![]()
(2)直线![]() 与
与![]() 轴、
轴、![]() 轴的交点A、B的坐标,分别为
轴的交点A、B的坐标,分别为![]()
所以OA=6,OB=3,则![]() ,
,
因为OA×OB=AB×OC,
所以![]()
![]()
(3)∵B关于![]() 轴的对称点
轴的对称点![]() ,连结
,连结![]() 交
交![]() 轴于Q,
轴于Q,
∴QP+QB的最小值为![]() ,
,
∵直线![]() 的解析式为
的解析式为![]() ,∴Q(0,3)
,∴Q(0,3)
(4)M(-1,0)或M(-2,0)或![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
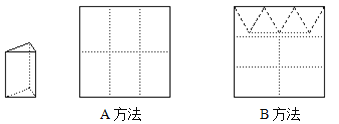
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
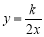 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。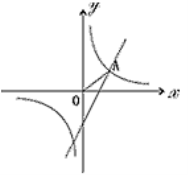
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上, 求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等边△ABC内接于⊙O,点P是劣弧
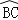 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.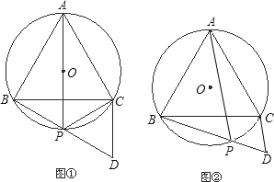
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
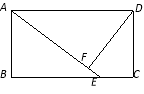
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC.
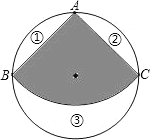
(1)求这个扇形的面积;
(2)若将扇形BAC围成一个圆锥的侧面,这个圆锥的底面直径是多少?能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
相关试题

