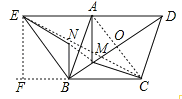
【题目】如图四边形ABCD是菱形，且∠ABC=60，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则下列五个结论中正确的是（　　）

①若菱形ABCD的边长为1，则AM+CM的最小值1；

②△AMB≌△ENB；

③S四边形AMBE=S四边形ADCM；

④连接AN，则AN⊥BE；

⑤当AM+BM+CM的最小值为2时，菱形ABCD的边长为2．

A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤

参考答案：

【答案】C

【解析】解：①连接AC，交BD于点O，∵四边形ABCD是菱形，∴AB=BC，BD⊥AC，AO=BO

∴点A，点C关于直线BD对称，∴M点与O点重合时AM+CM的值最小为AC的值

∵∠ABC=60，∴△ABC是等边三角形，∴AB=AC，∵AB=1，∴AC=1，即AM+CM的值最小为1，故①正确．

②∵△ABE是等边三角形，∴BA=BE，∠ABE=60°．

∵∠MBN=60°，∴∠MBN﹣∠ABN=∠ABE﹣∠ABN．

即∠MBA=∠NBE．

又∵MB=NB，∴△AMB≌△ENB（SAS），故②正确．

③∵S△ABE+S△ABM=S四边形AMBE

S△ACD+S△AMC=S四边形ADCM，且S△AMB≠S△AMC，∴S△ABE+S△ABM≠S△ACD+S△AMC，∴S四边形AMBE≠S四边形ADCM，故③错误．

④假设AN⊥BE，且AE=AB，∴AN是BE的垂直平分线，∴EN=BN=BM=MN，∴M点与O点重合，∵条件没有确定M点与O点重合，故④错误．

⑤如图，连接MN，由（1）知，△AMB≌△ENB，∴AM=EN，∵∠MBN=60°，MB=NB，∴△BMN是等边三角形，∴BM=MN，∴AM+BM+CM=EN+MN+CM．

根据“两点之间线段最短”，得EN+MN+CM=EC最短

∴当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长．

过E点作EF⊥BC交CB的延长线于F，∴∠EBF=180°﹣120°=60°，设菱形的边长为x，∴BF=x，EF=x，在Rt△EFC中，∵EF2+FC2=EC2，∴ ，解得x=2，故⑤正确．

综上所述，正确的答案是：①②⑤，故选C．

关闭