【题目】如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:(1)△APB≌△DPC;(2)∠BAP=2∠PAC.

参考答案:
【答案】证明见解析.
【解析】试题分析:根据正方形的性质和等腰三角形的性质得出∠ABP=∠DCP,再利用SAS判定三角形全等即可;(2)根据已知条件和正方形的性质得到△APD为等边三角形,求得∠DAP=60,即可分别求出∠PAC、∠BAP的度数,即可得到二者关系.
试题解析:
(1)∵四边形ABCD是正方形,∴∠ABC=∠DCB=90.
∵PB=PC,∴∠PBC=∠PCB.
∴∠ABC∠PBC=∠DCB∠PCB,即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.(3分)
(2)证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45.
∵△APB≌△DPC,∴AP=DP.
又∵AP=AB=AD,∴DP=AP=AD.
∴△APD是等边三角形。
∴∠DAP=60.
∴∠PAC=∠DAP∠DAC=15.
∴∠BAP=∠BAC∠PAC=30.
∴∠BAP=2∠PAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x﹣2)2+1
B.y=(x+2)2+1
C.y=(x﹣2)2﹣3
D.y=(x+2)2﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市去年约有50 000人参加中考,这个数据用科学记数法可表示为人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正五边形的每一个内角都等于°.
-
科目: 来源: 题型:
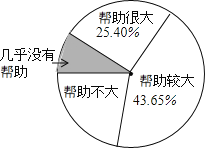
查看答案和解析>>【题目】为了解“数学思想作文对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和表来表示(图、表都没制作完成).
选项
帮助很大
帮助较大
帮助不大
几乎没有帮助
人数
a
543
269
b
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值.
(注:计算中涉及到的“人数”均精确到1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种80千克的钱,现在可买88千克。
(1)现在实际这种每千克多少元?
(2)准备这种,若这种的量y(千克)与单价x(元/千克)满足如图所示的一次函数关系。
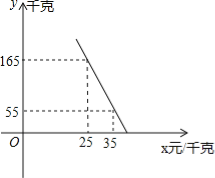
①求y与x之间的函数关系式;
②请你帮拿个主意,将这种的单价定为多少时,能获得最大利润?最大利润是多少?(利润=收入-进货金额)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人去水果批发市场采购苹果,他看中了
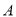 ,
, 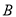 两家苹果,这两家苹果品质一样,零售价都为
两家苹果,这两家苹果品质一样,零售价都为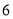 元/千克,批发价各不相同.
元/千克,批发价各不相同. 家规定:批发数量不超过
家规定:批发数量不超过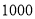 千克,按零售价的
千克,按零售价的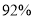 优惠;批发数量不超过
优惠;批发数量不超过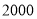 千克,按零售价的
千克,按零售价的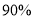 优惠;超过
优惠;超过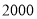 千克的按零售价的
千克的按零售价的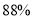 优惠。
优惠。 家的规定如下表:
家的规定如下表:数量范围(千克)
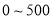 部分
部分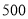 以上
以上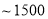 部分
部分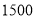 以上
以上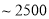 部分
部分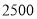 以上部分
以上部分价格(元)
零售价的
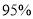
零售价的
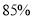
零售价的
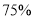
零售价的
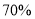
(
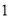 )如果他批发
)如果他批发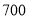 千克苹果,则他在
千克苹果,则他在 、
、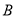 两家批发分别需要多少元?
两家批发分别需要多少元?(
 )如果他批发
)如果他批发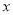 千克苹果
千克苹果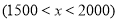 ,请你分别用含
,请你分别用含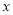 的代数式表示他在
的代数式表示他在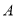 、
、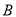 两家批发所需要的费用.
两家批发所需要的费用.(
 )现在他要批发
)现在他要批发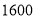 千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
相关试题

