【题目】 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;

(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)易证![]() ,从而可证到
,从而可证到![]() 即可得到
即可得到![]() 即
即![]() 由
由![]() 即可得到
即可得到![]()
(2)由![]() 可得
可得![]() 即可得到
即可得到![]() 从而可证到
从而可证到![]() 然后运用相似三角形的性质即可求出
然后运用相似三角形的性质即可求出![]() 的长.
的长.
试题解析:(1)∵ ∠APC=∠PAB+∠B,∠APD=∠B,
∴ ∠DPC=∠PAB.
又AB=AC,∴ ∠ABP=∠PCD,
∴ △ABP∽△PCD.
∴![]() =
=![]() ,∴
,∴ ![]() =
=![]() ,
,
∴ AC·CD=CP·BP.
(2)∵ PD∥AB,∴ ∠DPC=∠B,∠APD=∠PAB.
∵ ∠APD=∠B,∴ ∠PAB=∠B.
又∠B=∠C,∴ ∠PAB=∠C.
又∠PBA=∠ABC,∴ △PBA∽△ABC.
∴![]() =
=![]() ,∴ BP=
,∴ BP=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 ; (2)
; (2)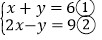 ;
;(3)
 ; (4)
; (4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.0的平方根是0B.5是25的算术平方根
C.﹣8的立方根是﹣2D.带根号的数都是无理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A.同位角相等
B.平行于同一直线的两条直线互相平行
C.两个锐角的和是锐角
D.和为180°的两个角互为邻补角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(1,0),B(3,2),将线段AB平移后得到线段CD,若点A的对应点C(2,﹣1),则点B的对应点D的坐标为( )
A.(4,1)B.(5,3)C.(5,1)D.(2,0)
相关试题

