【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.


参考答案:
【答案】见解析
【解析】分析:(1)用三角形的内角和定理判断∠D+∠B=180°;(2)连接EC,证明∠AEC+∠ACE+∠3+∠4=180°,根据同旁内角互补,两直线平行证明.
详解:(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
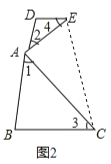
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
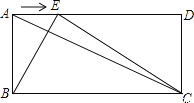
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 ; (2)
; (2)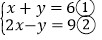 ;
;(3)
 ; (4)
; (4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.0的平方根是0B.5是25的算术平方根
C.﹣8的立方根是﹣2D.带根号的数都是无理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;

(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A.同位角相等
B.平行于同一直线的两条直线互相平行
C.两个锐角的和是锐角
D.和为180°的两个角互为邻补角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

相关试题

