【题目】某商店从厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价少20元,若购进甲商品5件和乙商品4件共需要1000元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件145元,乙种商品的售价为每件120元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于870元,则甲种商品至少可购进多少件?
参考答案:
【答案】(1)甲120元,乙100元;(2)14件
【解析】
1)设甲种商品每件进价是x元,乙种商品每件进价是y元,根据“乙商品每件进价比甲商品每件进价多20元,若购进甲商品5件和乙商品4件共需要1000元”列出方程组解答即可;
(2)设购进甲种商品a件,则乙种商品(40﹣a)件,根据“全部售出后总利润(利润=售价﹣进价)不少于870元”列出不等式解答即可.
(1)设甲商品进价每件x元,乙商品进价每件y元,根据题意得:
![]()
解得:![]() .
.
答:甲商品进价每件120元,乙商品进价每件100元.
(2)设甲商品购进a件,则乙商品购进(40﹣a)件
(145-120)a+(120-100)(40-a)≥870
∴a≥14.
∵a为整数,∴a至少为14.
答:甲商品至少购进14件.
-
科目: 来源: 题型:
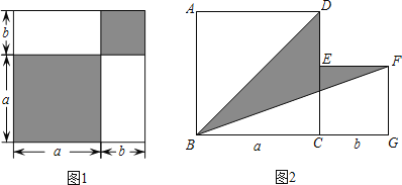
查看答案和解析>>【题目】请认真观察图形,解答下列问题:
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1:______;
方法2:______.
(2)从中你能发现什么结论?请用等式表示出来:______;
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为a、b,如果a+b=ab=4,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径, BM切⊙O于点B,点P是⊙O上的一个动点(不经过A,B两点),过O作OQ∥AP交
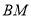 于点Q,过点P作
于点Q,过点P作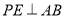 于C,交
于C,交 的延长线于点E,连结
的延长线于点E,连结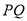 .
.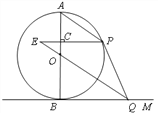
(1)求证:PQ与⊙O相切;
(2)若直径AB的长为12,PC=2EC,求tan∠E的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线
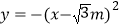 (m>0)的顶点为A,直线
(m>0)的顶点为A,直线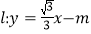 与
与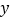 轴的交点为点B.
轴的交点为点B.(1)求出抛物线的对称轴及顶点A的坐标(用含
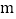 的代数式表示);
的代数式表示);(2)证明点A在直线
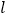 上,并求∠OAB的度数;
上,并求∠OAB的度数;(3)动点Q在抛物线对称轴上,问:抛物线上是否存在点P,使以点P、Q、A为顶点的三角形与△OAB全等?若存在,求出
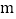 的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.
的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.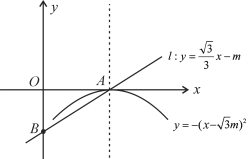
-
科目: 来源: 题型:
查看答案和解析>>【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
相关试题

