【题目】请认真观察图形,解答下列问题:
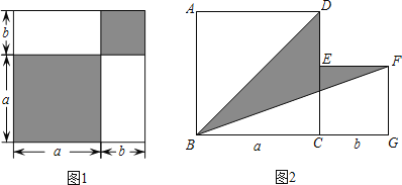
(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1:______;
方法2:______.
(2)从中你能发现什么结论?请用等式表示出来:______;
(3)利用(2)中结论解决下面的问题:
如图2,两个正方形边长分别为a、b,如果a+b=ab=4,求阴影部分的面积.
参考答案:
【答案】(1)a2+b2,(a+b)2-2ab;(2)a2+b2=(a+b)2-2ab;(3)阴影部分的面积=2.
【解析】
(1)方法1:两个正方形面积和,方法2:大正方形面积-两个小长方形面积;
(2)由题意可直接得到;
(3)由阴影部分面积=正方形ABCD的面积+正方形CGFE的面积-三角形ABD的面积-三角形BGF的面积,可求阴影部分的面积.
解:(1)由题意可得:方法1:a2+b2 方法2:(a+b)2-2ab,
故答案为:a2+b2,(a+b)2-2ab;
(2)a2+b2=(a+b)2-2ab,
故答案为:a2+b2=(a+b)2-2ab;
(3)∵阴影部分的面积=S正方形ABCD+S正方形CGFE-S△ABD-S△BGF=a2+b2-![]() a2-
a2-![]() (a+b)b
(a+b)b
∴阴影部分的面积=![]() a2+
a2+![]() b2-
b2-![]() ab=
ab=![]() [(a+b)2-2ab]-
[(a+b)2-2ab]-![]() ab,
ab,
∵a+b=ab=4,
∴阴影部分的面积=![]() [(a+b)2-2ab]-
[(a+b)2-2ab]-![]() ab=2.
ab=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ACB=90°,BC=AC,CE是过点C的一条直线,且A、B在CE的异侧,AD⊥CE于D,BE⊥CE于E.
(1)求证:AD=DE+BE.
(2)若直线CE绕点C旋转,使A、B在CE的同侧时(如图②),AD与DE、BE的关系如何?请予以证明.

-
科目: 来源: 题型:
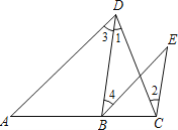
查看答案和解析>>【题目】已知:如图,∠1=∠2,∠3=∠E,试说明:∠A=∠EBC,(请按图填空,并补理由,)
证明:∵∠1=∠2(已知),
∴______∥______,________
∴∠E=∠______,________
又∵∠E=∠3(已知),
∴∠3=∠______(等量代换),
∴______∥______(内错角相等,两直线平行),
∴∠A=∠EBC,________
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设
 ,
, .
.①如图2,当点在线段BC上移动,则
 ,
, 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点在直线BC上移动,则
 ,
, 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店从厂家选购甲、乙两种商品,乙商品每件进价比甲商品每件进价少20元,若购进甲商品5件和乙商品4件共需要1000元;
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)若甲种商品的售价为每件145元,乙种商品的售价为每件120元,该商店准备购进甲、乙两种商品共40件,且这两种商品全部售出后总利润不少于870元,则甲种商品至少可购进多少件?
相关试题

