Question

【题目】如图，在平面直角坐标系中，直线y= x+1与抛物线y=ax2+bx﹣3交于A、B两点，点A在x轴上，点B的纵坐标为3．点P是直线AB下方的抛物线上一动点（不与A、B点重合），过点P作x轴的垂线交直线AB于点C，作PD⊥AB于点D．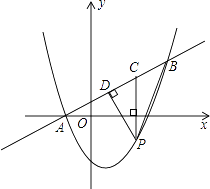

（1）求a、b及sin∠ACP的值；
（2）设点P的横坐标为m；
①用含有m的代数式表示线段PD的长，并求出线段PD长的最大值；
②连接PB，线段PC把△PDB分成两个三角形，是否存在适合的m的值，使这两个三角形的面积之比为9：10？若存在，直接写出m的值；若不存在，说明理由．

Answer 1

【答案】
（1）

解：由 x+1=0，得x=﹣2，∴A（﹣2，0）．

由 x+1=3，得x=4，∴B（4，3）．

∵y=ax2+bx﹣3经过A、B两点，

∴

∴ ，

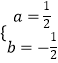则抛物线的解析式为：y= x2﹣ x﹣3，

设直线AB与y轴交于点E，则E（0，1）．

∵PC∥y轴，

∴∠ACP=∠AEO．

∴sin∠ACP=sin∠AEO= = =

（2）

解：①由（1）知，抛物线的解析式为y= x2﹣ x﹣3．则点P（m， m2﹣ m﹣3）．

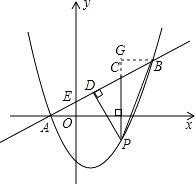
已知直线AB：y= x+1，则点C（m， m+1）．

∴PC= m+1﹣（ m2﹣ m﹣3）=﹣ m2+m+4=﹣ （m﹣1）2+

Rt△PCD中，PD=PCsin∠ACP=[﹣ （m﹣1）2+ ] =﹣ （m﹣1）2+

∴PD长的最大值为： ．

②如图，分别过点D、B作DF⊥PC，BG⊥PC，垂足分别为F、G．

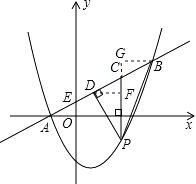
∵sin∠ACP= ，

∴cos∠ACP= ，

又∵∠FDP=∠ACP

∴cos∠FDP= = ，

在Rt△PDF中，DF= PD=﹣ （m2﹣2m﹣8）．

又∵BG=4﹣m，

∴ = = = = ．

当 = = 时，解得m= ；

当 = = 时，解得m= ．

【解析】（1）已知直线AB的解析式，首先能确定A、B点的坐标，然后利用待定系数法确定a、b的值；若设直线AB与y轴的交点为E，E点坐标易知，在Rt△AEO中，能求出sin∠AEO，而∠AEO=∠ACP，则∠ACP的正弦值可得．（2）①已知P点横坐标，根据直线AB、抛物线的解析式，求出C、P的坐标，由此得到线段PC的长；在Rt△PCD中，根据（1）中∠ACP的正弦值，即可求出PD的表达式，再根据所得函数的性质求出PD长的最大值．②在表达△PCD、△PBC的面积时，若都以PC为底，那么它们的面积比等于PC边上的高的比．分别过B、D作PC的垂线，首先求出这两条垂线段的表达式，然后根据题干给出的面积比例关系求出m的值．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．