【题目】某中学计划购买A型和B型课桌凳共200套.经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的 ![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
参考答案:
【答案】
(1)解:设A型每套x元,则B型每套(x+40)元.
由题意得:4x+5(x+40)=1820.
解得:x=180,x+40=220.
即购买一套A型课桌凳和一套B型课桌凳各需180元、220元
(2)解:设购买A型课桌凳a套,则购买B型课桌凳(200﹣a)套.
由题意得:  ,
,
解得:78≤a≤80.
∵a为整数,
∴a=78、79、80.
∴共有3种方案,
设购买课桌凳总费用为y元,
则y=180a+220(200﹣a)=﹣40a+44000.
∵﹣40<0,y随a的增大而减小,
∴当a=80时,总费用最低,此时200﹣a=120,
即总费用最低的方案是:购买A型80套,购买B型120套
【解析】(1)根据购买一套A型课桌凳比购买一套B型课桌凳少用40元,以及购买4套A型和5套B型课桌凳共需1820元,得出等式方程求出即可;(2)利用要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的 ![]() ,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆为庆祝开业,在楼前悬挂了许多宣传条幅.如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定.小明为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°.已知点C到大厦的距离BC=7米,∠ABD=90°.请根据以上数据求条幅的长度(结果保留整数.参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,则∠1+∠2的度数为( )

A. 80°; B. 90°; C. 100°; D. 110°;
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
(1)2x-{-3y+[3x-2(3x-y)]},其中x=-1,y=
 .
.(2)5(3a2b-ab2-1)-(ab2+3a2b-5),其中a=
 ,b=
,b= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整. 原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若
 =3,求
=3,求  的值.
的值.
(1)尝试探究 在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 , CG和EH的数量关系是 , 的值是 .
的值是 .
(2)类比延伸 如图2,在原题的条件下,若 =m(m>0),求
=m(m>0),求  的值(用含有m的代数式表示),试写出解答过程.
的值(用含有m的代数式表示),试写出解答过程.
(3)拓展迁移 如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F.若 =a,
=a,  =b,(a>0,b>0),则
=b,(a>0,b>0),则  的值是(用含a、b的代数式表示).
的值是(用含a、b的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】折叠三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC,若∠A=75°,∠C=60°,则∠BDF=____________________________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
 x+1与抛物线y=ax2+bx﹣3交于A、B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A、B点重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
x+1与抛物线y=ax2+bx﹣3交于A、B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A、B点重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.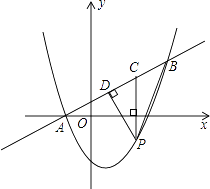
(1)求a、b及sin∠ACP的值;
(2)设点P的横坐标为m;
①用含有m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积之比为9:10?若存在,直接写出m的值;若不存在,说明理由.
相关试题

