【题目】如图1,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点A(0,3)、点C(-4,0).
(1)若把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,求折痕DE的长;
(2)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请直接写出点Q的坐标;若不存在,请说明理由;
(3)如图2,若M为AC边上的一动点,在OA上取一点N(0,1),将矩形OABC绕点O顺时针旋转一周,在旋转的过程中,M的对应点为M1,请直接写出NM1的最大值和最小值.

参考答案:
【答案】(1)![]() ;(2)当DE是菱形的对角线时,Q1(0,3),当DE是菱形的边时,Q2(
;(2)当DE是菱形的对角线时,Q1(0,3),当DE是菱形的边时,Q2(![]() ,3),Q3(-
,3),Q3(-![]() ,3),Q4(-
,3),Q4(-![]() ,-3);(3)最大值是5,最小值是
,-3);(3)最大值是5,最小值是![]() .
.
【解析】
(1)由△DFC∽△AOC,求出DF,再证明EF=DF;
(2)分两种情形分别讨论即可:①DE为菱形的边.②DE为菱形的对角线;
(3)由题意点M在如图3中的圆环内或两个圆上,利用图象法即可解决问题;
解:(1)解:(1)∵四边形OABC是矩形,
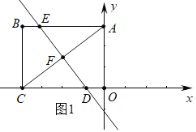
∴∠AOC=90°.
∵OA=3,OC=4,
∴AC=5.
由折叠可得:![]()
∵∠FCD=∠OCA,∠DFC=∠AOC=90°,
∴△DFC∽△AOC.
![]()
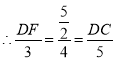
![]()
![]()
∵四边形OABC是矩形,
∴AB∥DC,
∴∠EAF=∠DCF
∴△AFE≌△CFD(ASA).
∴EF=DF.
![]()
∴折痕DE的长为![]()
(2)如下图,由(1)可知,![]()

![]()
当DE为菱形的边时,![]() ,可得
,可得![]() ;
;
当DE为菱形的对角线时,P与C重合,Q与A重合,Q2(0,3),
当点Q在第四象限,E与Q关于x轴对称,![]()
综上所述,满足条件的点Q坐标为![]() 或
或![]() 或(0,3)或
或(0,3)或![]() ;
;
(3)如图3中,作OH⊥AC,则![]()

观察图形可知,MN的最小值=OM-ON ![]() ;
;
MN的最大值=NM′=ON+OM′=1+4=5
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在综合与实践课上,老师组织同学们以“探索等腰三角形的边长与周长的关系”为主题展开数学活动.请你解决活动过程中产生的问题.
操作发现:已知
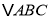 是等腰三角形.如果它的两条边长分别为
是等腰三角形.如果它的两条边长分别为 和
和 求它的周长.小明的做法是分为腰长为
求它的周长.小明的做法是分为腰长为 和
和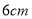 两种情况,进行计算.
两种情况,进行计算. 请你帮助小明补上计算过程;
请你帮助小明补上计算过程;继续探索:如果它的两条边长分别为
 和
和 求它的周长;
求它的周长; 此时它的周长还是两种结果吗?请说明理由,并求出此时等腰三角形的周长;
此时它的周长还是两种结果吗?请说明理由,并求出此时等腰三角形的周长;活学活用:
 如果它的周长为
如果它的周长为 一条边长为
一条边长为 则它的腰长为 .
则它的腰长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a﹣1时,函数值( )

A.y<0
B.0<y<m
C.y>m
D.y=m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AB=BC=2cm,
 与
与  关于点O中心对称,则AB、BC、
关于点O中心对称,则AB、BC、  、
、  所围成的图形的面积是cm2 .
所围成的图形的面积是cm2 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”
(1)请直接写出两个为“同簇二次函数”的函数:①______,②_________;
(2)已知关于
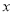 的二次函数
的二次函数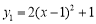 和
和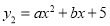 ,若
,若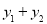 与
与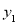 为“同簇二次函数”,求函数
为“同簇二次函数”,求函数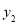 的表达式,并求出当
的表达式,并求出当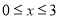 时,
时,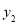 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
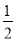 x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=
x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=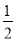 x﹣2上时,则△OAB平移的距离是_____.
x﹣2上时,则△OAB平移的距离是_____.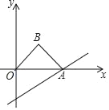
相关试题

