【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
参考答案:
【答案】(1)40;(2)72;(3)280.
【解析】
试题分析:(1)用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数;
(2)先计算出最想去D景点的人数,再补全条形统计图,然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)用800乘以样本中最想去A景点的人数所占的百分比即可.
试题解析:(1)被调查的学生总人数为8÷20%=40(人);
(2)最想去D景点的人数为40﹣8﹣14﹣4﹣6=8(人),补全条形统计图为:
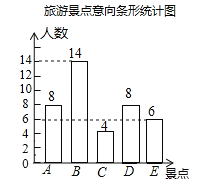
扇形统计图中表示“最想去景点D”的扇形圆心角的度数为![]() ×360°=72°;
×360°=72°;
(3)800×![]() =280,所以估计“最想去景点B“的学生人数为280人.
=280,所以估计“最想去景点B“的学生人数为280人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠A=∠B=∠C=∠D=90°)
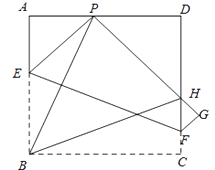
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,求出BE的长.(用含x的代数式表式) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
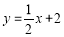 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线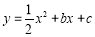 经过A、C两点,与x轴的另一交点为点B.
经过A、C两点,与x轴的另一交点为点B.(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为
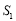 ,△BCE的面积为
,△BCE的面积为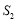 ,求
,求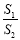 的最大值;
的最大值;②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=
 ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( )
A.①②
B.①③
C.②③
D.①③② -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
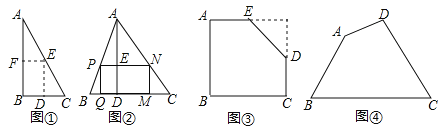
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=
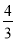 ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

相关试题

