【题目】在综合与实践课上,老师组织同学们以“探索等腰三角形的边长与周长的关系”为主题展开数学活动.请你解决活动过程中产生的问题.
操作发现:已知![]() 是等腰三角形.如果它的两条边长分别为
是等腰三角形.如果它的两条边长分别为![]() 和
和![]() 求它的周长.小明的做法是分为腰长为
求它的周长.小明的做法是分为腰长为![]() 和
和![]() 两种情况,进行计算.
两种情况,进行计算.
![]() 请你帮助小明补上计算过程;
请你帮助小明补上计算过程;
继续探索:如果它的两条边长分别为![]() 和
和![]() 求它的周长;
求它的周长;
![]() 此时它的周长还是两种结果吗?请说明理由,并求出此时等腰三角形的周长;
此时它的周长还是两种结果吗?请说明理由,并求出此时等腰三角形的周长;
活学活用:
![]() 如果它的周长为
如果它的周长为![]() 一条边长为
一条边长为![]() 则它的腰长为 .
则它的腰长为 .
参考答案:
【答案】(1)补充过程见解析;20cm;(2)不是,此时它的周长只有一种结果;22cm;(3)![]() 或
或![]() .
.
【解析】
(1)分当腰长为![]() 时和当腰长为
时和当腰长为![]() 时两种情况讨论,判断是否能够构成三角形,进而求出周长即可;
时两种情况讨论,判断是否能够构成三角形,进而求出周长即可;
(2)根据两边之和大于第三边,判断![]() 不能作为等腰三角形的腰,故只有一种结果;
不能作为等腰三角形的腰,故只有一种结果;
(3)分当![]() 是腰长时和当
是腰长时和当![]() 是底边长时两种情况讨论,判断是否能够构成三角形,进而求出腰长即可.
是底边长时两种情况讨论,判断是否能够构成三角形,进而求出腰长即可.
解:![]() 当腰长为
当腰长为![]() 时,
时,
![]() 的周长为
的周长为![]() .
.
当腰长为![]() 时,
时,
![]() 的周长为
的周长为![]() .
.
![]() 不是,此时它的周长只有一种结果.(回答不是即给分)
不是,此时它的周长只有一种结果.(回答不是即给分)
理由如下:![]() 当腰长为
当腰长为![]() 时,
时,![]()
不满足“两边之和大于第三边”,
此时,![]() 的周长为
的周长为![]() .
.
![]() 当
当![]() 是腰长时,则底边长为17-7-7=3,三边分别为7,7,3,可以构成三角形.
是腰长时,则底边长为17-7-7=3,三边分别为7,7,3,可以构成三角形.
当![]() 是底边长时,则腰长为
是底边长时,则腰长为![]() =5,三边分别为5,5,7,可以构成三角形.
=5,三边分别为5,5,7,可以构成三角形.
∴它的腰长为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形中,由三角形的内角平分线所形成的角存在一定的规律,理解并掌握其中的规律,有助于同学们巩固相关的数学知识.
如图1,
 中,
中, 分别平分
分别平分 ,且相交于点
,且相交于点 “勤奋小组”的同学发现:
“勤奋小组”的同学发现: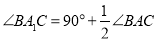 .证明过程如下:
.证明过程如下:
证明:如图2,连接
 并延长,
并延长,
则
 (依据1)
(依据1) 与
与 分别平分
分别平分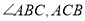
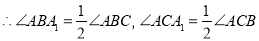




又
 ,(依据2)
,(依据2) .
. 依据1是 ___,依据2是 __;
依据1是 ___,依据2是 __; 如图3,在图1的基础上,作
如图3,在图1的基础上,作 的角平分线
的角平分线 交于点
交于点 试探究
试探究 与
与 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水池有甲、乙、丙三个水管,其中甲、丙两管为进水管,乙管为出水管.单位时间内,甲管水流量最大,丙管水流量最小.先开甲、乙两管,一段时间后,关闭乙管开丙管,又经过一段时间,关闭甲管开乙管.则能正确反映水池蓄水量y(立方米)随时间t(小时)变化的图象是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“父亲节”的临近,某商场决定开展“感恩父爱,回馈顾客”的促销活动,对部分节日大礼包进行打折销售.其中
 款节日大礼包打
款节日大礼包打 折
折 款节日大礼包打
款节日大礼包打 折.已知打折前,购买
折.已知打折前,购买 盒
盒 款节日大礼包和
款节日大礼包和 盒
盒 款节日大礼包需要
款节日大礼包需要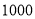 元;打折后买
元;打折后买 盒
盒 款节日大礼包和
款节日大礼包和 盒
盒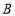 款节日大礼包需要
款节日大礼包需要 元.
元. 求打折后
求打折后 两款节日大礼包每盒分别为多少元?
两款节日大礼包每盒分别为多少元? 打折期间,某公司计划为员工采购
打折期间,某公司计划为员工采购 盒节日大礼包,总费用不超过
盒节日大礼包,总费用不超过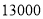 元,则最多可以购买
元,则最多可以购买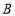 款节日大礼包多少盒?
款节日大礼包多少盒? -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a﹣1时,函数值( )

A.y<0
B.0<y<m
C.y>m
D.y=m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AB=BC=2cm,
 与
与  关于点O中心对称,则AB、BC、
关于点O中心对称,则AB、BC、  、
、  所围成的图形的面积是cm2 .
所围成的图形的面积是cm2 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点A(0,3)、点C(-4,0).
(1)若把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,求折痕DE的长;
(2)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请直接写出点Q的坐标;若不存在,请说明理由;
(3)如图2,若M为AC边上的一动点,在OA上取一点N(0,1),将矩形OABC绕点O顺时针旋转一周,在旋转的过程中,M的对应点为M1,请直接写出NM1的最大值和最小值.

相关试题

