【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
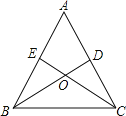
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
参考答案:
【答案】D
【解析】
试题分析:根据三角形的内角和等于180°求出∠ABC+∠ACB=120°,再根据角平分线的性质求出∠OBC+∠OCB=60°,然后利用三角形的内角和等于180°列式计算即可求出∠BOC的度数;
连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,根据角平分线上的点到角的两边的距离相等可得OF=OG=OH,从而可得△BOF和△BOH全等,△COG和△COH全等,根据全等三角形对应边相等可得BH=BF,CH=CG,再根据四边形的内角和求出∠FOG=120°,根据对顶角相等求出∠EOD=120°,然后推出∠EOF=∠DOG,再利用“角边角”证明△EOF和△DOG全等,根据全等三角形对应边相等可得EF=DG,OD=OE,即可判定出B、C选项都正确,根据等角对等边的性质,只有∠ABC=∠ACB时才能得到OB=OC,所以D选项错误.
解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°,
∵△ABC的两条角平分线BD、CE交于O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣![]() (∠ABC+∠ACB)=120°,故A选项正确;
(∠ABC+∠ACB)=120°,故A选项正确;
如图,连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,
∵△ABC的两条角平分线BD、CE交于O,
∴OF=OG=OH,
利用“HL”可得△BOF≌△BOH,△COG≌△COH,
∴BH=BF,CH=CG,
在四边形AFOG中,∠FOG=360°﹣60°﹣90°×2=120°,
∴DOG=∠FOG﹣∠DOF=120°﹣∠DOF,
又∵∠EOD=∠BOC=120°,
∴∠EOF=∠EOD﹣∠DOF=120°﹣∠DOF,
∴∠EOF=∠DOG,
在△EOF和△DOG中,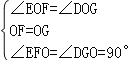 ,
,
∴△EOF≌△DOG(ASA),
∴EF=DG,OD=OE,故C选项正确;
∴BC=BH+CH=BF+CG=BE+EF+CD﹣DG=BE+CD,
即BC=BE+CD,故B选项正确;
只有当∠ABC=∠ACB时,∵△ABC的两条角平分线BD、CE交于O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
而本题无法得到∠ABC=∠ACB,
所以,OB=OC不正确,故D选项错误.
故选D.
-
科目: 来源: 题型:
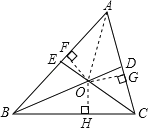
查看答案和解析>>【题目】如图,△ABC和△DBE都是等腰直角三角形,点D在AC上,其中∠ABC=∠DBE=90°.
(1)求∠DCE的度数;
(2)当AB=5,AD:DC=2:3时,求DE的大小;
(3)当点D在线段AC上运动时(D不与A重合),请写出一个反映DA2,DC2,DB2之间关系的等式,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,点O为坐标原点,点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,且OB=2OA,OBOC=OCOA=2.
(1)求点C的坐标;
(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,设点P运动的时间为t(t>0)秒,线段PQ的长度为y,用含t的式子表示y,并写出相应的t的范围;
(3)在(2)的条件下,过点P作x轴的垂线PM,PM=PQ,是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
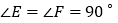 ,
,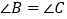 ,
,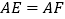 ,给出下列结论:①
,给出下列结论:①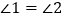 ;②
;②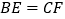 ;③
;③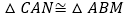 ;④
;④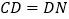 .其中正确的结论是( )
.其中正确的结论是( )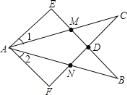
A. ①② B. ②③ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知将
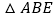 沿
沿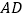 所在直线翻折,点
所在直线翻折,点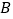 恰好与
恰好与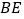 上的点
上的点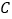 重合,对折边
重合,对折边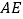 ,折痕也经过点
,折痕也经过点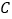 ,则下列说法正确的是( )
,则下列说法正确的是( )①
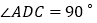 ;
;②
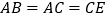 ;
;③
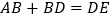 ;
;④
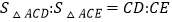 ;
;⑤若
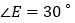 ,则
,则 是等边三角形.
是等边三角形.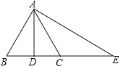
A. 只有①②正确 B. ①②③
C. ①②③④ D. ①②③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,除公共边
 外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使
外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使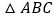 与
与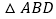 全等:
全等: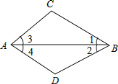
 ________,________
________,________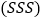 ;
;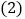 ________,________
________,________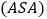 ;
;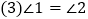 ,________
,________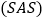 ;
;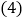 ________,
________,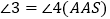 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】点
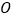 是
是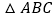 内一点,且点
内一点,且点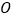 到三边的距离相等,
到三边的距离相等,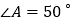 ,则
,则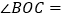 ________.
________.
相关试题

