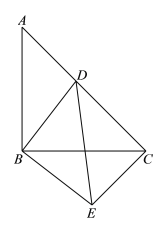
【题目】如图,△ABC和△DBE都是等腰直角三角形,点D在AC上,其中∠ABC=∠DBE=90°.
(1)求∠DCE的度数;
(2)当AB=5,AD:DC=2:3时,求DE的大小;
(3)当点D在线段AC上运动时(D不与A重合),请写出一个反映DA2,DC2,DB2之间关系的等式,并加以证明.
参考答案:
【答案】(1)∠DCE=90°;(2)![]() ;(3)2BD2=DA2+DC2,证明见解析.
;(3)2BD2=DA2+DC2,证明见解析.
【解析】
(1)由已知条件不难证明△ABD≌△CBE,可得∠A=∠ACB=∠BCE=45°,所以∠DCE=90°;(2)由AB=5可得AC=5![]() ,由AD:DC=2:3可以分别求出AD、CD的长度,进而求出CE的长度,利用勾股定理求出DE的长度即可;(3)由△BDE是等腰直角三角形,可得DE=
,由AD:DC=2:3可以分别求出AD、CD的长度,进而求出CE的长度,利用勾股定理求出DE的长度即可;(3)由△BDE是等腰直角三角形,可得DE=![]() BD,因为AD=CE,所以DE2=DC2+CE2=AD2+CD2,所以2BD2=AD2+CD2.
BD,因为AD=CE,所以DE2=DC2+CE2=AD2+CD2,所以2BD2=AD2+CD2.
(1)∵等腰直角△ABC,
∴AB=AC,∠ABC=90°,∠A=∠ACB=45°,
同理可得:DE=BE,∠DBE=90°,∠BDE=∠BED=45°,
∴∠ABD=∠CBE,
∵在△ABD与△CBE中,
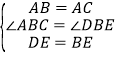 ,
,
∴△ABD≌△CBE,
∴∠A=∠ACB=∠BCE=45°,∠ABD=∠CBE,AD=CE,
∴∠DCE=90°;
(2)当AB=5,AD:DC=2:3时,有AC=![]() ,AD=
,AD=![]() ,DC=
,DC=![]() ,
,
在Rt△DCE中,CD=![]() ,CE=AD=
,CE=AD=![]() ,由勾股定理可得DE=
,由勾股定理可得DE=![]() ;
;
(3)2BD2=DA2+DC2;
∵△BDE是等腰直角三角形,
∴DE=![]() BD,
BD,
∵AD=CE,
∴DE2=DC2+CE2=AD2+CD2,
故2BD2=AD2+CD2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东昌湖举行的健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所滑行的路程y(m)与实践x(min)之间的函数关系如图所示,下列说法正确的有____________.
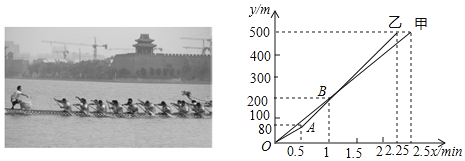
①乙队比甲队提前0. 25min到达终点.
②当乙队划行110m时,此时落后甲队15m.
③0. 5min后,乙队比甲队每分钟快40m.
④自1. 5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把三角形AE折叠,使点D恰好落在BC边上,设此点为F,若三角形ABF的面积为24,那么CE长度为__________cm2.

-
科目: 来源: 题型:
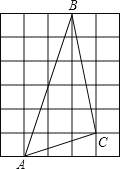
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形,若点A(x,
 ),点B(2x1,
),点B(2x1,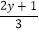 ),点C(z+1,
),点C(z+1,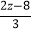 ),已知点A,B关于原点对称,点C在二,四象限平分线上.
),已知点A,B关于原点对称,点C在二,四象限平分线上. (1)求A、B、C点的坐标;
(2)结合A、B、C的坐标,在图中建立平面直角坐标系;
(3)在(2)的条件下,若P为y轴上的一个动点,请直接写出使△PBC周长最小的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,点O为坐标原点,点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,且OB=2OA,OBOC=OCOA=2.
(1)求点C的坐标;
(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,设点P运动的时间为t(t>0)秒,线段PQ的长度为y,用含t的式子表示y,并写出相应的t的范围;
(3)在(2)的条件下,过点P作x轴的垂线PM,PM=PQ,是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
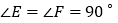 ,
,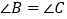 ,
,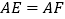 ,给出下列结论:①
,给出下列结论:①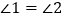 ;②
;②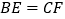 ;③
;③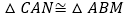 ;④
;④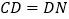 .其中正确的结论是( )
.其中正确的结论是( )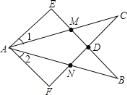
A. ①② B. ②③ C. ①②③ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
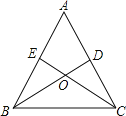
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
相关试题

