【题目】点![]() 是
是![]() 内一点,且点
内一点,且点![]() 到三边的距离相等,
到三边的距离相等,![]() ,则
,则![]() ________.
________.
参考答案:
【答案】![]()
【解析】
根据三角形内角和定理求出∠ABC+∠ACB=130°,再根据角平分线上的点到角的两边的距离相等判断出点O是△ABC角平分线的交点,再根据角平分线的定义求出∠OBC+∠OCB的度数,然后在△OBC中,利用三角形内角和定理列式进行计算即可得解.
如图,

∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵点O到△ABC三边的距离相等,
∴点O是△ABC角平分线的交点,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°=65°,
×130°=65°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°.
故答案为:115°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
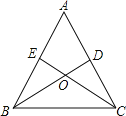
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知将
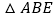 沿
沿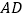 所在直线翻折,点
所在直线翻折,点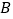 恰好与
恰好与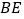 上的点
上的点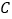 重合,对折边
重合,对折边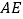 ,折痕也经过点
,折痕也经过点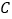 ,则下列说法正确的是( )
,则下列说法正确的是( )①
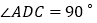 ;
;②
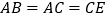 ;
;③
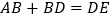 ;
;④
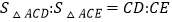 ;
;⑤若
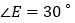 ,则
,则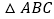 是等边三角形.
是等边三角形.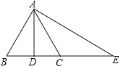
A. 只有①②正确 B. ①②③
C. ①②③④ D. ①②③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,除公共边
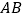 外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使
外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使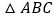 与
与 全等:
全等: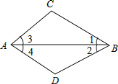
 ________,________
________,________ ;
;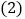 ________,________
________,________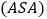 ;
;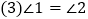 ,________
,________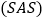 ;
;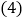 ________,
________,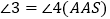 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
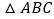 中,若
中,若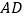 是
是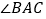 的角平分线,点
的角平分线,点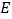 和点
和点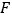 分别在
分别在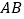 和
和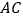 上,且
上,且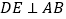 ,垂足为
,垂足为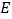 ,
,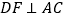 ,垂足为
,垂足为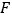 (如图
(如图 ),则可以得到以下两个结论:
),则可以得到以下两个结论:①
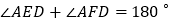 ;②
;②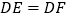 .
.那么在
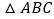 中,仍然有条件“
中,仍然有条件“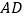 是
是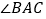 的角平分线,点
的角平分线,点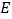 和点
和点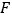 ,分别在
,分别在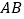 和
和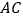 上”,请探究以下两个问题:
上”,请探究以下两个问题: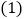 若
若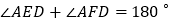 (如图
(如图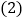 ),则
),则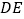 与
与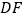 是否仍相等?若仍相等,请证明;否则请举出反例.
是否仍相等?若仍相等,请证明;否则请举出反例.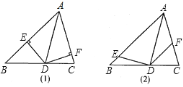
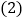 若
若 ,则
,则 是否成立?(只写出结论,不证明)
是否成立?(只写出结论,不证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C为半圆上一点,AD平分∠CAB交⊙O于点D

(1)求证:OD∥AC;
(2)若AC=8,AB=10,求AD. -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
相关试题

